Condensed Matter Physics

crystallographic restriction translational periodicity aperiodic lattice six-fold symmetry (60^o) possible without overlaps five-fold symmetry (72^o) would lead to atoms encroaching on each other

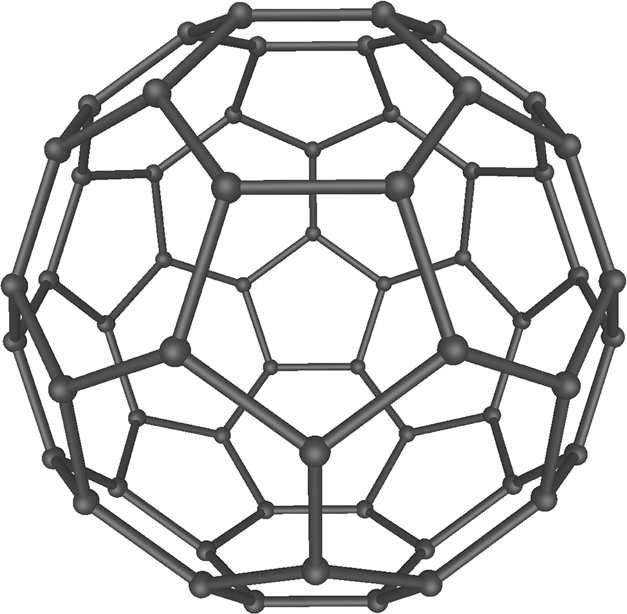
Five-fold symmetry is possible in finite and non-periodic structures such as Buckminsterfullerene, C₆₀

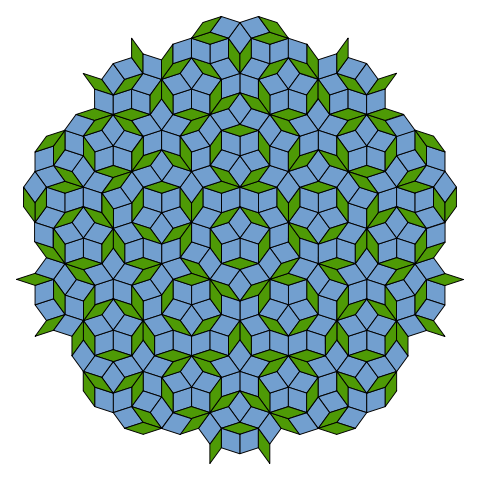
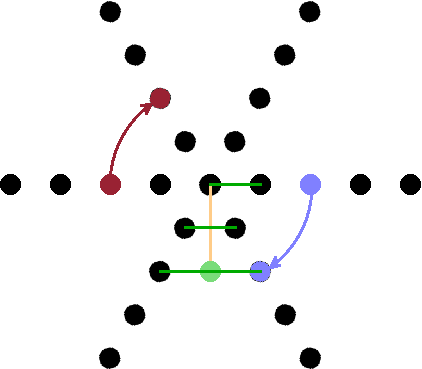
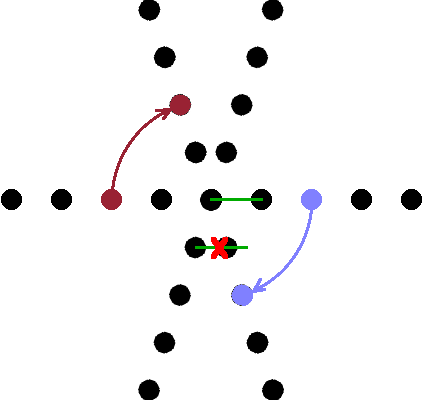
tilings self-similarity inflation - deflation Tilings made from two different types of tile can be regular but aperiodic.

But not all such tilings are aperiodic: The arrangement shown here has ordinary crystalline translational periodicity.

Crystal - quasicrystal single crystal - single-grain quasicrystal

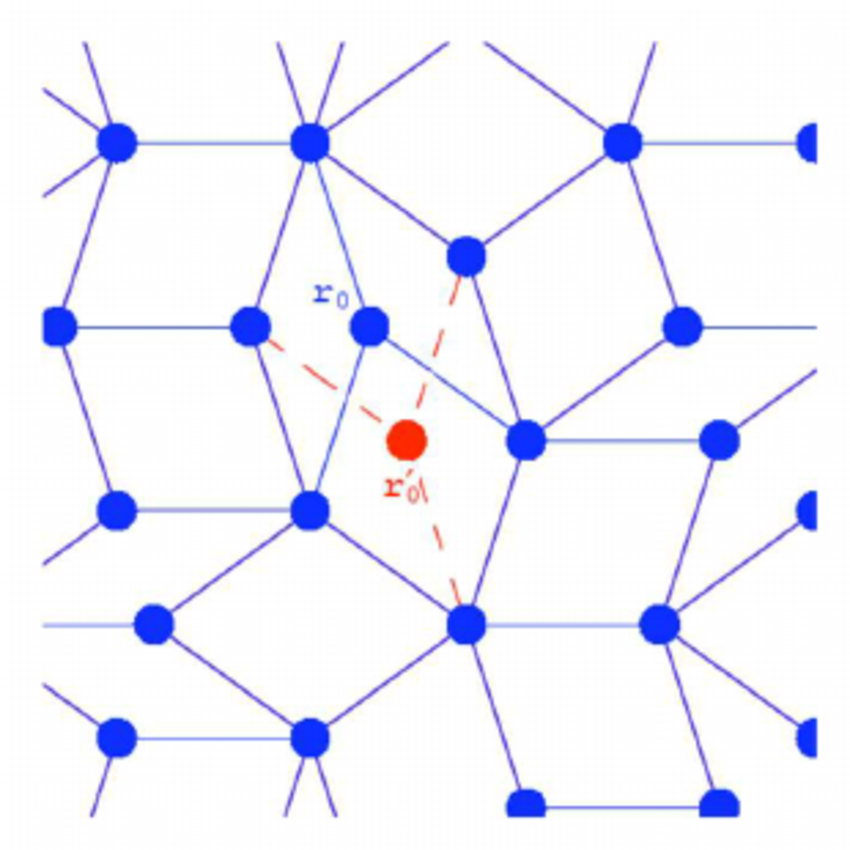
phonons - phasons

electron diffraction 10-fold (or 5-fold or 8-fold) symmetry periodic in the other two directions Dan Shechtman, Nobel prize for chemistry, 2011 icosahedral quasi-crystals aperiodic in all three dimensions

defects exist in quasicrystals as they do in crystals. The diagram above is a simulation showing the disorder of a two-dimensional quasi-crystal (tiling) increasing as the temperature rises.

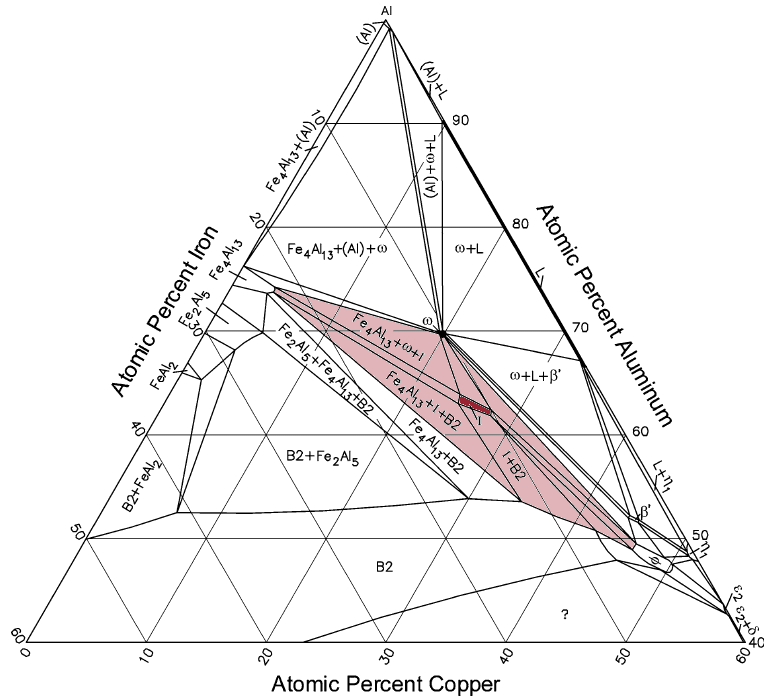
Many quasicrystalline materials are ternary alloys, often involving aluminium. The phase diagram shows the small area of thermodynamic stability of the quasi-crystalline phase in the system Al-Cu-Fe (dark red). Adjacent to it are two-phase regions where the quasi-crystal phase is in equilibrium with various crystalline compounds (light red).