
Two field quantities are used to describe the shape of a magnetic field, the B-field and the H-field. Traditionally, they are named magnetic field, $\vec{H}$, and magnetic flux density or magnetic induction, $\vec{B}$ but this suggests a causal relationship of the two rather than one of interaction, which is more appropriate. The H-field represents the field produced by a current running in a conductor; it is therefore measured in A/m. The B-field is measured in T(esla). In vacuum, the two are linked by a universal constant of proportionality, the permeability, $\mu_0$ = 1.26×10-6 H/m (=Tm/A), which takes care of the conversion of units: $$\vec{B}=\mu_0\vec{H}\qquad.$$
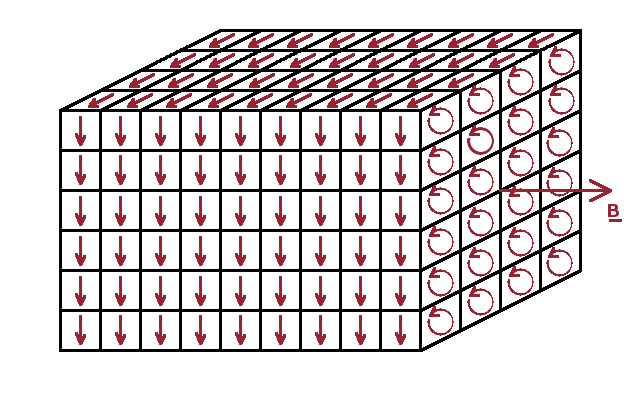
When a material is placed in a magnetic field, the field interacts with the electrons in the material. Like all moving charges, the electrons are subject to the Lorentz force, which accelerates (i.e. deflects) them at right angles with both their trajectory and the field. We can envisage a slab of material as consisting of many small cells. Then there will be a small eddy current in each of those cells because the external field forces the electrons to circulate around it. Since these bound currents cancel each other out where neighbouring eddies are in contact, the only macroscopic current is a surface current around the outer surface of the object.
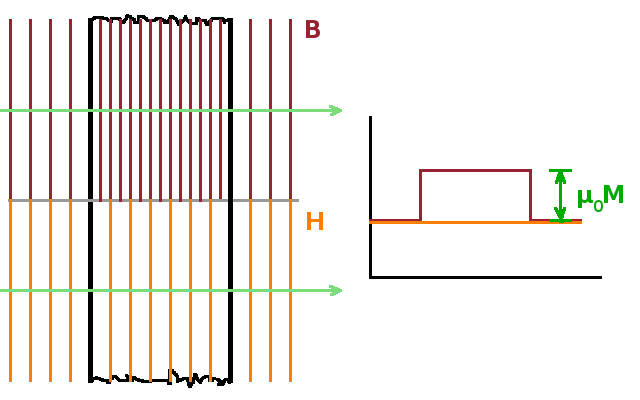
The H-field is induced only by macroscopic (net) currents, while bound currents are also sources of the B-field. This means that, in a material, the simple relationship between $\vec{H}$ and $\vec{B}$ breaks down. While the component of the H-field tangential to a long magnetic rod does not change at its surface (bottom half of figure), the tangential component of the B-field has a step there, indicated in the figure by a different density of B-field lines inside and outside the material. The graph shows cross sections of both fields across the rod. The difference between the two fields is the magnetisation, $\vec{M}$: $$\vec{B}=\mu_0(\vec{H}+\vec{M})$$ Like the H-field, magnetisation is a vector and is measured in A/m. It is the vector sum of the magnetic moments of each atom in the sample, normalised to the sample volume: $$\vec{M}=\frac{\sum_i\vec{p}_{m,i}}{V}$$
Since the magnitude of the magnetisation depends on the material, it is logical to restore the link between B-field and H-field by introducing a material constant which describes to what extent B-field lines are drawn into or out of a material. This is the (dimensionless) relative permeability, $\mu_{rel}$, of the material: $$\vec{B}=\mu_0\mu_{rel}\vec{H}$$ Since relative permeabilities are very close to 1 for many materials, it is often easier to consider the material's susceptibility, $\chi:=\mu_{rel}-1$ instead: $$\vec{B}=\mu_0(1+\chi)\vec{H}$$
Depending on the value of the susceptibility, materials are grouped into three classes:
It is important to note that these different material classes are not identical with the three underlying mechanisms, which will be discussed in the following. All materials are diamagnetic, but in para- and ferromagnetics the para- or ferromagnetic effect overcompensates the diamagnetism. In order to be able to show ferromagnetism, a material must be paramagnetic.
Over the next few sections, we will look at dia- and paramagnetism in more detail, see how conduction electrons in metals affect paramagnetism, and investigate why magnetism in ferromagnets is so much stronger.