
| magnetic | electric | |||
|---|---|---|---|---|
| $\vec{B}=\mu_0\mu_r(\vec{H}+\vec{M})$ | $\vec{D}=\epsilon_0\epsilon_r\vec{E}+\vec{P}$ | |||
| $\vec{H}$ | magnetic field | $\vec{E}$ | electric field | |
| $\vec{B}$ | magnetic flux density | $\vec{D}$ | displacement field | |
| $\vec{M}$ | magnetisation | $\vec{P}$ | polarisation | |
| $\mu_0$ | vacuum permeability | $\epsilon_0$ | vacuum permittivity | |
| $\mu_r$ | relative permeability | $\epsilon_r$ | relative permittivity | |
| $p_m$ | magnetic moment | $p$ | dipole moment | |
Magnetic and electric phenomena in solids are closely related, and it is possible to extend the concepts we know from magnetism to understand how materials behave in electric fields. There is a direct correspondence between magnetic and electric quantities as shown in the table. The only difference is that the polarisation is measured in the same units as the displacement field, the equivalent of the B-field rather than the H-field.
As is the case in magnetism, there are electric states of matter characterised by temporary, induced dipole moments (dielectrics) and ones involving permanent charge separations with resulting permanent dipole moments (paraelectrics). There are also states of collective electricity, where permanent dipoles are coupled strongly enough to influence each other and to form domains of uniform polarisation (ferroelectrics), including the variants with antiparallel (antiferroelectrics) or uneven (ferrielectrics) alignment. These are named by analogy with their magnetic equivalents; despite the fact that iron, after which these properties are named, does not show any of them.
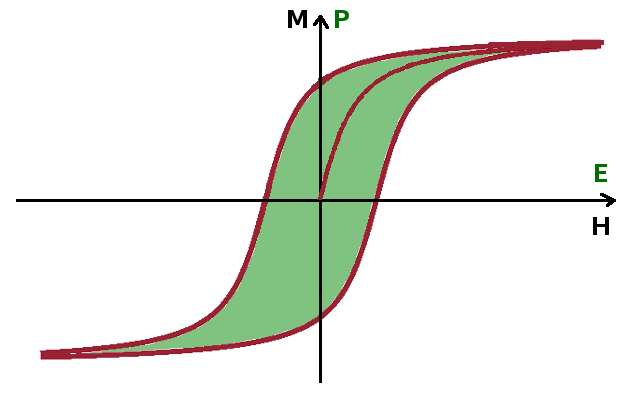
The susceptibility is defined in the same way both in electric and magnetic terms (i.e. the difference between the permeability/permittivity and 1), and the Curie law and Curie-Weiss law for its temperature dependence, $$\chi_{\textrm{para}}=\frac{C}{T(-T_C)}\qquad,$$ is the same along with the Curie constant, $C$, and the Curie temperature, $T_C$. Polarisation and electric field show the same hysteretic behaviour as magnetisation and H-field.
This concludes the core part of this course. In the parallel optional module, we'll return to crystal structures to investigate defects and disorder in crystalline materials.