Mae'r holl differynnau mewn hafaliad differol cyffredin (HDC) yn ddifferynnau a pherthynas i'r un newidyn, h.y. nid yw HDC yn cynnwys unrhyw differynnau gwahaniaethol megys
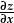 .
.
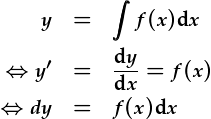
Adnabyddir HDC o'r ffurf 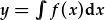 fel HDC gwahaniaethol oherwydd y termau y a mae modd rhannu'r termau x ar yr ochr chwith a'r dde o'r hafaliad trwy integreiddio'n uniongyrchol. Sylwch y gall f(x) fod yn unrhyw ffwythiant o x (cyn belled fod modd ei integreiddio), ond ni ddylir fod unrhyw perthynas efo y.
fel HDC gwahaniaethol oherwydd y termau y a mae modd rhannu'r termau x ar yr ochr chwith a'r dde o'r hafaliad trwy integreiddio'n uniongyrchol. Sylwch y gall f(x) fod yn unrhyw ffwythiant o x (cyn belled fod modd ei integreiddio), ond ni ddylir fod unrhyw perthynas efo y.
Yn ffiseg, does dim rheidrwydd i'r newidion cael eu galw'n x, y, z... Os oes angen, gallwch gyfieithu'r hafaliad ffisegol gan ddefnyddio'r ffurf x, y, z.
Er enghraifft, cysudrwch darfodiad ymbelydrol. Arsylwad: mae'r cyfradd darfodiad yn gymesur i'r nifer o'r atomau.
| Nodiant ffisegol | Nodiant rhywogaethol | ||
|---|---|---|---|
| Nifer yr atomau | N | - newidyn dibynnol | y |
| amser | t | - newidyn annibynnol | x |
| cyfradd darfodiad | 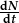 |
- differyn | 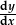 |
| cysonyn cymesurol | 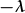 |
- paramedr | c |
| HDC i'w ddatrys: | 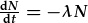 |
- | 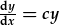 |
| gwahanwch: | 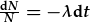 |
- | 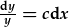 |
| integreiddiwch: | 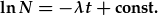 |
- | 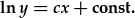 |
| Datrys ar gyfer N: | 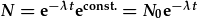 |
- (neu ar gyfer y) | 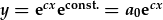 |
| nifer cychwynnol o atomau | N0 | - mesur terfynol | a0 |
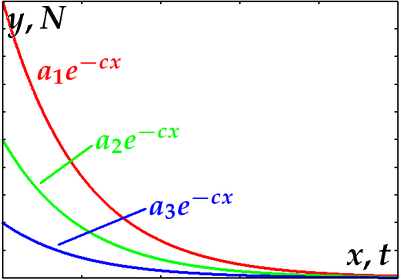
Nid oes un datrysiad unigryw, ond dosbarth cyfan o ddatrysiadau sy'n dibynnu ar y dewis o mesuriadau cychwynnol a terfynol, h.y. yn dibynnu ar faint o ddeunydd ymbelydrol oedd yn bresenol yn y cychwyn.
| Ffurf cyffredinol HDC gradd 1af llinol yw | 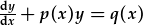 . . |
| Yr hafaliad cyfatebol homogenaidd yw | 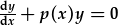 , , |
| sydd modd ei wahanu: | 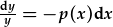 , , |
| integreiddio: | 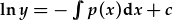 , , |
| a'i ddatrys y: | 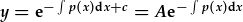 (1), (1), |
| lle | 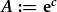 . . |
| Gan adael yr integreiddyn yn yr esbonyddyn | 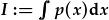 |
| a differu: | 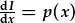 (2). (2). |
| Amnewid (2) i (1): | 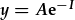 , which looks much friendlier! , which looks much friendlier! |
| Aildrefnu: | 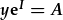 |
| a differu: | 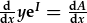 . . |
| Gweithredu'r rheol cadwyn i'r ochr chwith: | 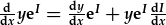 , , |
| amnewid (2) fewn iddo ac aildrefnu: | 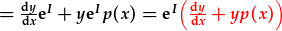 . . |
| Mae'r rhan wedi'i amlygu yr un fath a'r HDC cychwynol, a gallwn ei amnewid fewn i'r hafaliad olaf: | 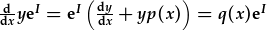 . . |
| Integreiddio: | 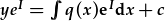 . That's it. . That's it. |
Wrth gwrs, does dim rhaid gwneud hyn bob tro mae angen datrys HDC gradd 1af llinol.
| Pan mae hafaliad o'r ffurf | 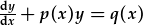 , , |
| mae'n syml i ffeindio'r ffactor integreiddio | 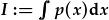 |
| ac yna datrys | 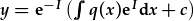 , , |
ble mae c yn gysonyn integreiddio sydd modd ei osod os oes amodau terfynol ffisegol addas ar gael.
Os nad yw HDC yn wahaniaethol neu llinol, gallwch ymgeisio ei ffitio i batrymau eraill. Patrwm cyffredin yw'r math Bernoulli, sydd yn HDC gradd 1af llinol gyda pwerau uwch o'r newidyn dibynnol (h.y. nid yw'n llwyr llinol yn ol ein diffiniad ni).
| Dyma hafaliad cyffredinol Bernoulli: | 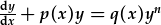 . . |
| Gadewch | 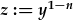 |
| a differu: |
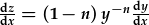
|
| (gan fod | 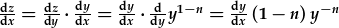 ). ). |
Lluoswch yr hafliad gwreiddiol gan 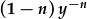 : : |
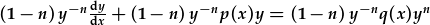 , , |
| Cyfunwch y termau y: |
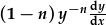
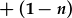
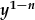
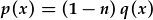 . .
|
| ac amnewid z and z': | 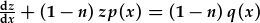 . . |
Mae hwn yn HDC gradd 1af llwyr llinol, a gellir ei ddatrys fel a ddisgrifir uchod. Datryswch ar gyfer z(x) ac ailamnewidiwch i ffeindio y(x). Peidiwch anghofio'r cynffactor (1-n)o flaen y p(x) a q(x)!
Yn yr achosion blaenorol, roedd p(x) a q(x) yn ffwythiannau o'r newidyn annibynnol yn unig. Yma, rydym yn ymlacio'r honiad yma ac yn ysgrifennu p(x,y) a q(x,y). Ond sylwer nad ddylir y ffwythiannau yma cynnwys unrhyw differynnau.
| Dyma hafaliad homogenaidd cyffredinol: | 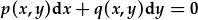 . . |
| Gallwn ailysgrifennu hwn fel |
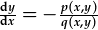 ,
sydd yn fwy tebygol o godi'i ben ta beth. ,
sydd yn fwy tebygol o godi'i ben ta beth.
|
Gan ddiffinio 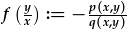 , mae gennym , mae gennym |
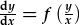 . . |
Gan hefyd ddiffinio 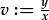 : : |
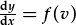 a y=vx. a y=vx. |
| Differu: |
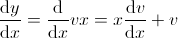
|
| Datrys ar gyfer dv/dx: |
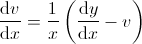
|
| ac amnewid: | 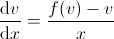 , , |
| sydd modd ei wahanu: | 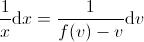 . . |
Datrys ar gyfer v(x) ac ailamnewid.
Mae'r technegau yma'n ddigonol i ddatrys y mwyafrif o HDC. Fe trafodir math arall, HDC llinol o unrhyw radd gyda cyfernodau cyson, nes ymlaen. Nawr, beth am ddarganfod syt i sefydlu amodau terfynol.
Ar y pwynt yma, byddech o bosib yn hoffi trio'r taflen waith cyntaf. Gwiriwch eich datrysiadau ar ol gorffen.