Gradd hafaliad differol yw'r gradd uchaf o unrhyw differyn mae'n ei gynnwys.
Esiamplau:
Mae 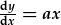 yn radd 1af,
yn radd 1af,
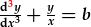 yn 3ydd radd, a
yn 3ydd radd, a
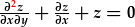 yn 2il radd.
yn 2il radd.
Mae hafaliad differol cyffredin (HDC) yn cynnwys differynion gyda pherthynas i un newidyn yn unig, mae hafaliadau differol rhannol (HDR) yn cynnwys differynion gyda pherthynas i nifer o newidion annibynnol.
Esiamplau:
Mae 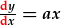 a
a
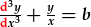 yn HDC, ond
yn HDC, ond
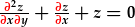 a
a
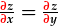 yn HDR.
yn HDR.
Sylwch fod y 'd' syth neu cyrliog, os yn cael eu defnyddio'n gywir, yn gwahaniaethu rhwng HDC a HDR. Y gwir brawf yw os yw'r newidyn dibynnol yn dibynnu ar un neu fwy o newidion annibynnol. Yn yr esiamplau uchod, mae gennym y(x) ond z(x,y).
Nid yw hafaliadau differol llinol yn cynnwys unrhyw pwerau uwch o unrhyw differynion, mae hafaliadau differol aflinol yn cynnwys pwerau uwch. Mewn hafaliadau differol llwyr llinol, nid oes pwerau uwch o'r newidyn(ion) annibynnol.
Esiamplau:
Mae'r esiamplau uchod yn llinol, ond dydi
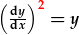 ddim.
Nodwch fod
ddim.
Nodwch fod 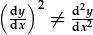 !
!
Mae hafaliad differol yn homogenaidd os nad yw'r cynnwys termau annifferol ac yn heterogenaidd os yw.
Esiamplau:
Mae 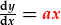 a
a
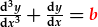 yn heterogenaidd (os nad yw'r cyfernodau a a b yn sero), ond mae
yn heterogenaidd (os nad yw'r cyfernodau a a b yn sero), ond mae
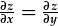 yn homogenaidd.
yn homogenaidd.
Mae ochr dde sero yn arwydd o hafaliad differol homogenaidd wedi ei dacluso, ond gwyliwch am dermau annifferol wedi eu cuddio ar yr ochr chwith!
Fel rheol, mae datrys hafaliadau differol heterogenaidd yn golygu ffeindio datrysiad i'r hafaliad homogenaidd cyfatebol fel cam hanner ffordd.