Hafaliad ton 2 - dau set o amodau terfyn :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

Plycio a tharo tant/llinyn

Fig.: llinyn wedi ei hoelio ar x=0 a x=l yn dirgrynnu ag osgled h.

Gellir taro neu plycio tannau offeryn cerdd i ddechrau dirgryniad, gan gynhyrchu --os ydym yn lwcus-- nodyn. Mae gitarydd yn plycio tant ond pianydd yn defnyddio'r morthwylion bach o fewn y piano i daro tannau. Y gwahaniaeth yw fod yr osgiliadau rhydd yn dechrau pan fod gitarydd yn rhyddhau'r tant mewn safle i ffwrdd o'i safle cyfantol, tra bod y morthwyl yn y piano yn taro tant yn y safle cyfantol. Yn yr un modd, mae tant gitar yn cyflymu tuag at y safle cyfantol, tra bod tant y piano ar ei gyflymder uchaf cyn gynted a mae'r morthwyl yn taro, yna mae'n arafu wrth symud tuag at ei osgled fwyaf.

Fel pendilwm, mae'r tant yn osgileiddio rhwng stad o egni cinetig mwyaf (pan mae'n pasio trwy'r safle cyfantol) a egni potensial mwyaf (ar yr osgled mwyaf). Pan mae tant yn cael ei blycio, mae'n cychwyn ei osgled yn y stad egni-potensial; pan mae tant yn cael ei daro, mae'n cychwyn yn y stad egni-cinetig.

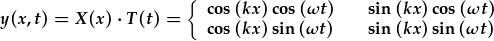Datrysiadau cyffredinol yr hafaliad don yw:	$y(x,t)={\cos{kx}\cos{kvt};\sin{kx}\cos{kvt};\cos{kx}\sin{kvt};\sin{kx}\sin{kvt}}$ .
Fe hoelir y dant ar x=0 ac ar x=l:	y(0,t)=y(l,t)=0.
Felly bydd hanner cyfnod unrhyw osgiliad yn lluosrif o hyd y dant,
i.e. amod ton sefydlog:	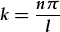$k=\frac{n\pi}{l}$ .
Hefyd, nid yw'r datrysiadau cos(kx) yn boddhau y(0,t)=0:	$y(x,t)={\sin{kx}\cos{kvt};\sin{kx}\sin{kvt}}$ .

Mae'r amodau terfyn eraill yn dibynnu os yw'r tant ar gitar neu piano:

wedi'i blycio (gitar)	wedi'i daro (piano)
Amod terfyn safleol:
dechrau ar osgled mwyaf: y(x,0)=f(x)	dechrau ar safle cyfantol: y(x,0)=0
Amod terfyn cyflymder (differol):
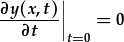
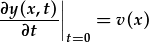
dim symudiad cyn rhyddhau'r dant: $\frac{\partial y(x,t)}{\partial t}\|_{t=0}=0$	cyflymder mwyaf wrth rhyddhau: $\frac{\partial y(x,t)}{\partial t}\|_{t=0}=v(x)$
Ton sin neu cosin mewn amser yw'r datrysiad. Mae'r cyflymder, ei ddeilliad gydag amser, felly'n don cosin neu sin. Mae'r cyflymder yn 0 ar t=0; felly ton sin yw. Felly rhaid i'r datrysiad fod a ffurf cosin mewn amser.	Mae y(x,0)=0 yn gofyn am datrysiad sin mewn amser.
Dewis o datrysiad cyffredinol:
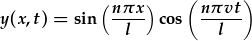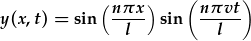$y(x,t)=\sin{\frac{n\pi x}{l}\cos{\frac{n\pi vt}{l}}}$	$y(x,t)=\sin{\frac{n\pi x}{l}\sin{\frac{n\pi vt}{l}}}$
Ehangu i cyfres sin:
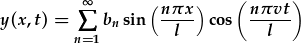
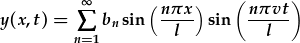
$y(x,t)=\sum_{n=1}^{\infty}b_n\sin{\frac{n\pi x}{l}\cos{\frac{n\pi vt}{l}}}$	$y(x,t)=\sum_{n=1}^{\infty}b_n\sin{\frac{n\pi x}{l}\sin{\frac{n\pi vt}{l}}}$
Gan gofio'r amod terfyn...:
y(x,0)=f(x)	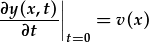$\frac{\partial y(x,t)}{\partial t}\|_{t=0}=v(x)$
...ac amnewid:
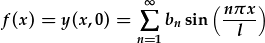$f(x)=y(x,0)=\sum_{n=1}^{\infty}b_n\sin{\frac{n\pi x}{l}}$	Yma mae rhaid differuy(x,t) cyn cymhwyso'r amod terfyn differol: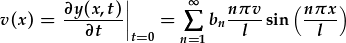 $v(x)=\frac{\partial y(x,t)}{\partial t}\|_{t=0}=\sum_{n=1}^{\infty}b_n\frac{n\pi v}{l}\sin{\frac{n\pi x}{l}}$

Cedwir ffeindio'r cyfernodau Fourier ar gyfer y tant sy'n cael ei hitio ar gyfer gweithdy. Defnyddiwch y talfyriad 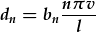$d_n=b_n\frac{n\pi v}{l}$ yna datryswch yr integreiddiad Fourier fel arfer.

Cyfernodau Fourier ar gyfer y dant sy'n cael ei blycio

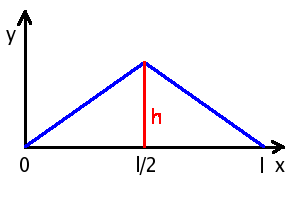
Gellir gweld y ffwythiant f(x) sy'n disgrifio safle'r dant cyn ei rhyddhau] (h.y. ar t=0) yn y diagram uchod.

Fel y gwelwn, yr amod terfyn safleol yw:

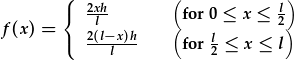$f(x)={\frac{2xh}{l} for 0\leq x\leq\frac{l}{2};\frac{2(l-x)h}{l}) for \frac{l}{2}\leq x\leq l}$ .

I ffeindio'r cyfernodau Fourier, datryswch: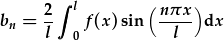

$b_n=\frac{2}{l}\int_0^lf(x)\sin{\frac{n\pi x}{l}}dx$ .

Amnewid f(x):

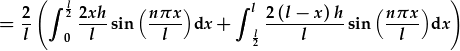
$=\frac{2}{l}(\int_0^{\frac{l}{2}}\frac{2xh}{l}\sin{\frac{n\pi x}{l}}dx+\int_{\frac{l}{2}}^l\frac{2(l-x)h}{l}\sin{\frac{n\pi x}{l}}dx)$

a symud y cysonion o flaen yr integreiddion:

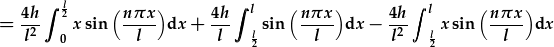$=\frac{4h}{l^2}\int_0^{\frac{l}{2}}x\sin{\frac{n\pi x}{l}}dx+\frac{4h}{l}\int_{\frac{l}{2}}^l\sin{\frac{n\pi x}{l}}dx-\frac{4h}{l^2}\int_{\frac{l}{2}}^lx\sin{\frac{n\pi x}{l}}dx$ .

Mae'r trydydd integreiddiad a'r cyntaf yn unfath (heblaw am y terfynnau).

Gellir ei integreiddio mewn rhannau:

$\int x\sin{(\frac{n\pi x}{l})}\ur{d}x$	$=x\int\sin{(\frac{n\pi x}{l})}\ur{d}x-\int\int\sin{(\frac{n\pi x}{l})}\ur{d}^2x$
	$=-\frac{xl}{n\pi}\cos{(\frac{n\pi x}{l})}+\frac{l}{n\pi}\int\cos{(\frac{n\pi x}{l})}\ur{d}x$
	$=-\frac{xl}{n\pi}\cos{(\frac{n\pi x}{l})}+\frac{l^2}{n^2\pi^2}\sin{(\frac{n\pi x}{l})}$

Felly, datrys integreiddiad yn yr hafaliad b_n:

$=-\frac{4hl}{l^2n\pi}\left[x\cos{(\frac{n\pi x}{l})}\right]_0^{\frac{l}{2}}+\frac{4hl^2}{l^2n^2\pi^2}\left[\sin{(\frac{n\pi x}{l})}\right]_0^{\frac{l}{2}}$

$-\frac{4hl}{ln\pi}\left[\cos{(\frac{n\pi x}{l})}\right]_{\frac{l}{2}}^l+\frac{4hl}{l^2n\pi}\left[x\cos{(\frac{n\pi x}{l})}\right]_{\frac{l}{2}}^l-\frac{4hl^2}{l^2n^2\pi^2}\left[\sin{(\frac{n\pi x}{l})}\right]_{\frac{l}{2}}^l$ ,

amnewid terfynau:

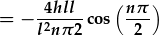
$=-\frac{4hll}{l^2n\pi 2}\cos{(\frac{n\pi}{2})}$

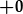
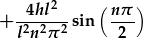
$+\frac{4hl^2}{l^2n^2\pi^2}\sin{(\frac{n\pi}{2})}$

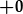
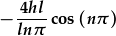
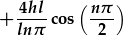
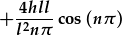
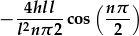
$-\frac{4hl}{ln\pi}\cos{(n\pi)}$ $+\frac{4hl}{ln\pi}\cos{(\frac{n\pi}{2})}$ $+\frac{4hll}{l^2n\pi}\cos{(n\pi)}$ $-\frac{4hll}{l^2n\pi 2}\cos{(\frac{n\pi}{2})}$

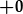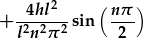, $+\frac{4hl^2}{l^2n^2\pi^2}\sin{(\frac{n\pi}{2})}$ ,

a thacluso:

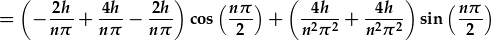
$=(-\frac{2h}{n\pi}+\frac{4h}{n\pi}-\frac{2h}{n\pi})\cos{(\frac{n\pi}{2})}+(\frac{4h}{n^2\pi^2}+\frac{4h}{n^2\pi^2})\sin{(\frac{n\pi}{2})}$

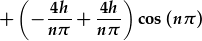$+(-\frac{4h}{n\pi}+\frac{4h}{n\pi})\cos{(n\pi)}$ .

Mae mwyafrif y cyfernodau yn canslo, felly: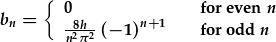

$b_n={0 i n gwastad; \frac{8h}{n^2\pi^2}(-1)^{n+1} i n od}$ .

Mae'r ffactor (-1)ⁿ⁺¹ yn galluogi arwydd sy'n newid bob yn ail. I orffen,

amnewid y b_n fewn i y(x,t):

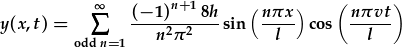$y(x,t)=\sum_{odd n=1}^{\infty}\frac{(-1)^{n+1}8h}{n^2\pi^2}\sin{\frac{n\pi x}{l}}\cos{\frac{n\pi vt}{l}}$ .

Yr hafaliad don mewn mwy nag un dimensiwn

Mae problemau o'r fath yma'n gofyn am ddefnydd o cyfesurynnau pegynol er mwyn defnyddio eu cymesuredd naturiol. Rhaid trin y dimensiynau gofodol ychwanegol drwy gwahaniadau ychwanegol ar ol gwahanu'r dibynniaeth amser.

Hafaliad don cyffredinol:	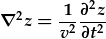$\del^2z=\frac{1}{v^2}\frac{\partial^2z}{\partial t^2}$
Gwahanu'r rhan amser:	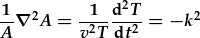$\frac{1}{A}\nabla^2A=\frac{1}{v^2T}\frac{d^2T}{dt^2}=-k^2$ ,
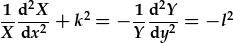then separate x and y:	$\frac{1}{X}\frac{d^2X}{dx^2}+k^2=-\frac{1}{Y}\frac{d^2Y}{dy^2}=-l^2$ .

Mae hyn yn gorffen yr adran ar hafaliadau differol, ond mae gweithdy 4 ar ol i'w gwblhau. Gwiriwch eich datrysiadau wedyn.

Wedi ein cyflwyno i gyfres Fourier, cam bach yw delio gyda trawsffurfiadau Fourier, techneg hynod o bwysig yn ffiseg.