Hafaliad Laplace 3 - ehangiad Fourier :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

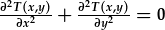Rydym wedi ffeindio datrysiadau cyffredinol hafaliad Laplace,	$\frac{\partial^2T(x,y)}{\partial x^2}+\frac{\partial^2T(x,y)}{\partial y^2}=0$ .
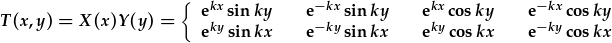
Y datrysiadau cyffredinol yw: $T(x,y)=X(x)Y(y)={e^{kx}\sin{ky};e^{-kx}\sin{ky};e^{kx}\cos{ky};e^{-kx}\cos{ky}}$
Gan gymhwyso amodau terfyn y broblem plat poeth fe geir	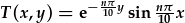$T(x,y)=e^{-\frac{n\pi}{10}y}\sin{\frac{n\pi}{10}x}$
fel datrysiadau sy'n gwneud synhwyr ffisegol.
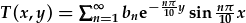Cyfuniad llinol o'r cyfernodau b_n is	$T(x,y)=\sum_{n=1}^{\infty}b_ne^{-\frac{n\pi}{10}y}\sin{\frac{n\pi}{10}x}$ .

Cymharwch y cyfuniad llinol uchod gyda'r gyfres Fourier sin:	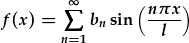$f(x)=\sum_{n=1}^{\infty}b_n\sin{\frac{n\pi x}{l}}$ .
Maent yn unfath ar gyfer l=10 a y=0 (oherwydd bod y term e yw 1).
Mae'r AT ar gyfer yr ochr sy'n cael ei gynhesu heb ei ddefnyddio eto:	T(x,0)=100.
Felly, gallwn amnewid:	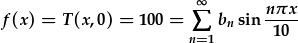$f(x)=T(x,0)=100=\sum_{n=1}^{\infty}b_n\sin{\frac{n\pi x}{10}}$ .
Y cyfernodau Fourier yw, yn gyffredinol:	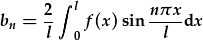$b_n=\frac{2}{l}\int_0^lf(x)\sin{\frac{n\pi x}{l}}dx$ .
Felly yn yr achos yma:	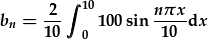$b_n=\frac{2}{10}\int_0^{10}100\sin{\frac{n\pi x}{10}}dx$ .
Integreiddio:	$=20(-\frac{10}{n\pi})[\cos{\frac{n\pi x}{10}}]_0^{10}$ ,
gosod cyfyngiadau:	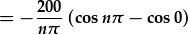$=-\frac{200}{n\pi}(\cos{n\pi}-\cos{0})$ ,
a thacluso:	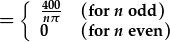$={\frac{400}{n\pi} (n od); 0 (n gwastad)}$ .
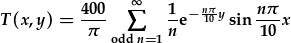I orffen, gosod y b_n fewn i T(x,y):	$T(x,y)=\frac{400}{\pi}\sum_{odd n=1}^{\infty}\frac{1}{n}e^{-\frac{n\pi}{10}y}\sin{\frac{n\pi}{10}x}$ .

A __dyna fe__ !

Datrysiad cyffredinol
1. $\nabla^2T=0$
2. gwahanu newidion: T(x,y)=X(x)·Y(y)
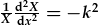
3. yn arwain i'r HDR ail radd: $\frac{1}{X}\frac{d^2X}{dx^2}=-k^2$
4. a'i datrys fel HDC gyda cyfernodau cyson: $T(x,y)=e^{\pm kx}[\sin|\cos](ky)$
Datrysiad penodol
1. gymhwyso amodau terfyn i ddiddymu termau sin/cos/esbonyddol anffisegol
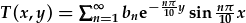2. aileirio'r datrysiad fel cyfuniad llunol o harmoniau: $T(x,y)=\sum_{n=1}^{\infty}b_ne^{-\frac{n\pi}{10}y}\sin{\frac{n\pi}{10}x}$ (neu debyg)
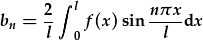
3. ffeindio'r cyfernodau Fourier: $b_n=\frac{2}{l}\int_0^lf(x)\sin{\frac{n\pi x}{l}}dx$

Yr eitem nesaf ar y rhestr o HDR mewn ffiseg yw'r hafaliad trylediad.