Trawsffurfiad Fourier 3 - trawsffurfio ymarfero :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

Mae'r dudalen hwn yn cynnwys nifer o esiamplau sy'n ymdebygu data parth-amser a gasglwyd gan spectromedr trawsffurfiad-Fourier, o'r math sy'n cael ei ddefnyddio ar gyfer soniaredd niwclear magnetig (SNM) neu spectroscopi isgoch (IG). Mae signal nodweddiadol yn darfod yn esbonyddol gyda arosodiad o sawl osgiliad. Yn y trawsffurfiad Fourier o'r data, mae'r darfod yn trawsffurfio i lled y llinell, tra bod yr osgiliadau yn dangos fel safleoedd y llinell, h.y. y spectrwm. Os oes gennych gnuplot neu MathCAD neu debyg, gallwch drio hwn gartref; Mae taflen waith yma yn rhoi cyfarwyddiadau.

Darfodiad esbonyddol unigol

Mae darfod esbonyddol unigol real yn unig	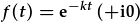$f(t)=e^{-kt}(+i0)$
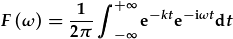yn trawsffurfio fel	$F(\omega)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}e^{-kt}e^{-i\omega t}dt$ .

Os gadewn i'r echel amser gychwyn ar sero, a, o pwynt a ymlaen, mae'r signal mwy ne lai yn sero,

yna mae'r cyfyngau yn	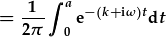$=\frac{1}{2\pi}\int_0^ae^{-(k+i\omega)t}dt$ .
Integreiddio:	$=\frac{1}{2\pi}[-\frac{1}{k+i\omega}e^{-(k+i\omega)t}]_0^a$ ,
amnewid cyfyngau:	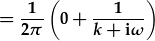$=\frac{1}{2\pi}(0+\frac{1}{k+i\omega})$
(mae'r term cyntaf yn sero trwy ddiffiniad a fel gwerth torri ffwrdd).
Tacluso:	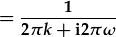$=\frac{1}{2\pi k+i2\pi\omega}$ .
I weld rhannau real a dychmygol y datrysiad, mae'n well diddymu'r uned cymhlyg yn yr enwadur. Gellir wneud hyn drwy lluosi yr enwebydd a'r enwadur gyda cyfiau yr enwadur:
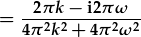	$=\frac{2\pi k-i2\pi\omega}{4\pi^2k^2+4\pi^2\omega^2}$ .
Tacluso eto:	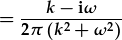$=\frac{k-i\omega}{2\pi(k^2+\omega^2}$ .

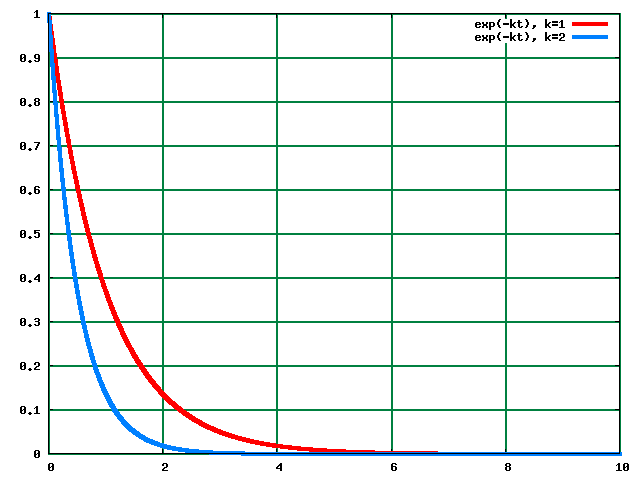Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

Cymharwch dau darfodiad esbonyddol, un araf (k=1) ac un cyflym (k=2).
Nodwch fod y spectrwm yn gymhlyg er fod y data parth-amser yn llwyr real!
Mae'r rhan real yn linell cymesurol tra bod y rhan dychmygol yn anghymesurol. Mewn spectroscopeg, mae'r siapau yma'n cael eu nabod fel llinellau amsugnol a gwasgarol.
Darfod arafach - spectrwm culhach. Mae hwn yn rhinwedd pwysig o parau trawsffurfiad Fourier: Pan mae un yn cynnyddu, mae'r llall yn lleihau gan eu bod yn gilyddol. Meddyliwch Fourier!

Syfliad cydwedd

Yn yr esiampl uchod, roedd y ffwythiant mewnbwn yn real yn unig. Yn gyffredinol, mi fydd yna ffactor cydwedd sy'n penderfynu beth yw dosbarthiad yr arddwysedd rhwng y rhannau real a dychmygol.

Ffwythiant darfod gyda ffactor cydwedd:	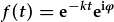$f(t)=e^{-kt}e^{i\phi}$ ,
sydd yr un fath a	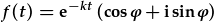$f(t)=e^{-kt}(\cos\phi+i\sin\phi)$ ,
h.y. modyleiddwyd y rhannau real a dychmygol gan don cosin a sin yn ol eu trefn.
Dyma'r trawsffurfiad Fourier:	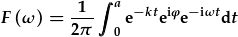$F(\omega)=\frac{1}{2\pi}\int_0^ae^{-kt}e^{i\phi}e^{-i\omega t}dt$ .
Nid yw'r ffactor cydwedd yn dibynnu ar t. Felly,	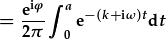$=\frac{e^{i\phi}}{2\pi}\int_0^ae^{-(k+i\omega)t}dt$ ,
sy'n cynnwyr yr un integriad a'r uchod:	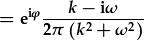$=e^{i\phi}\frac{k-i\omega}{2\pi(k^2+\omega^2)}$ .

Canlyniad hyn yw'r signalau parth-amser a'r spectrymau canlynol:

Dim syfliad cydwedd.

Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

Hwn yw'r ffwythiant mewnbwn real yn unig gwreiddiol unwaith eto.
Mae'r mewnosodiad yn dangos ble mae'r data mewn plân cymhlyg.
Cliciwch ar y ddelwedd i drawsffurfio'n Fourier.

cydwedd=π/6

Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

As the phase angle increases, intensity is shuffled from the real part into the imaginary part and then back.
As a consequence, the line shapes aren't pure absorption or dispersion lines any more.

cydwedd=π/4

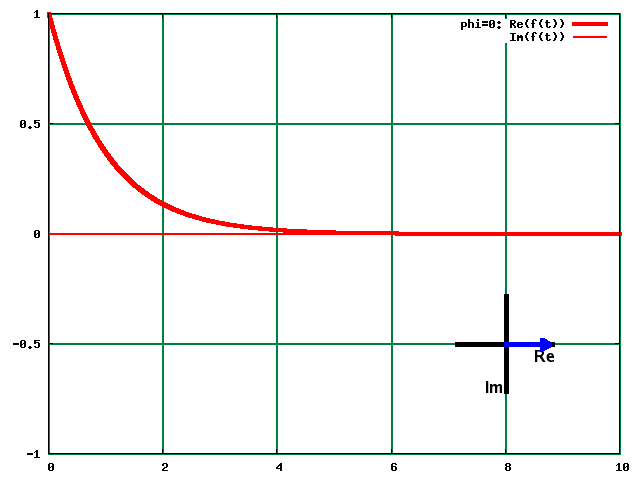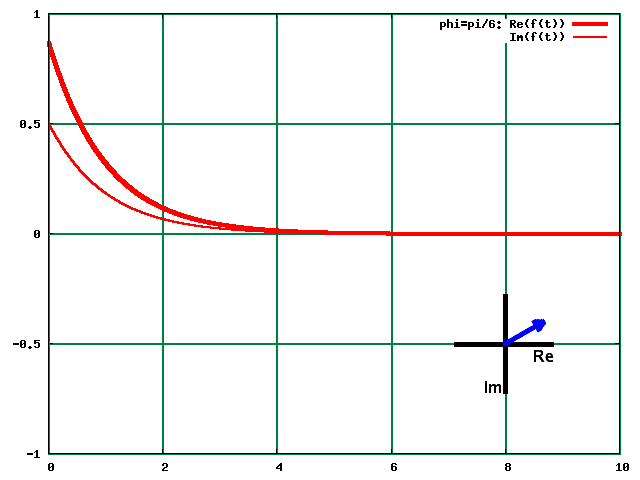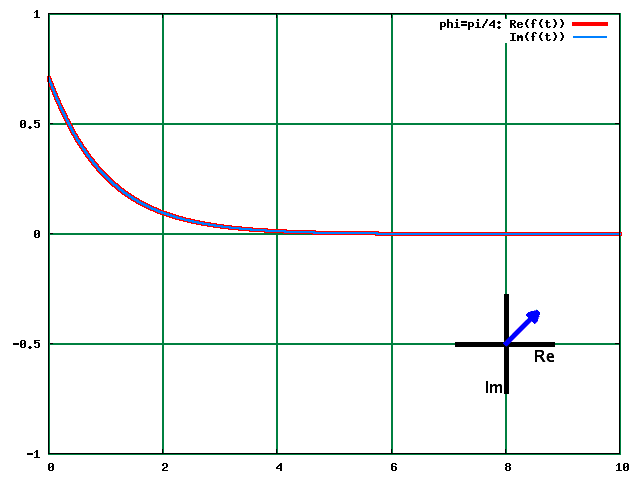Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

Ar π/4, mae rhannau real a dychmygol y ffwythiant mewnbwn yn unfath. Yn y spectrwm cyfatebol, mae'r llinellau real a dychmygol yn ddrych-delweddau o'u gilydd. Mae'r drych yn gyfochrog i'r echel y ar safle'r llinell (yma mae x=0).

cydwedd=π/2

Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

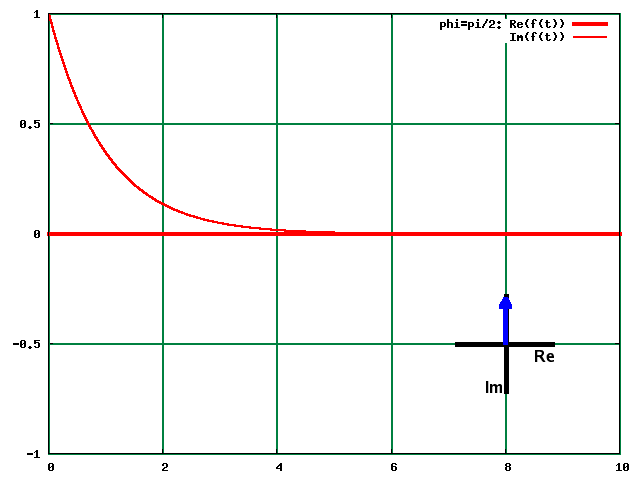
Ar π/2, mae'r rhannau real a dychmygol wedi eu amnewid gyda pherthynas i'r ffwythiannau gwreiddiol. Yn y spectrwm, mae'r ddau cydran yn amnewid hefyd. Nodwch fod y rhan real nawr yn drych-ddelwedd o'r rhan dychmygol gwreiddiol (oherwydd fod Im yn canlyn Re o π/2 o hyd).

cydwedd=π

Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

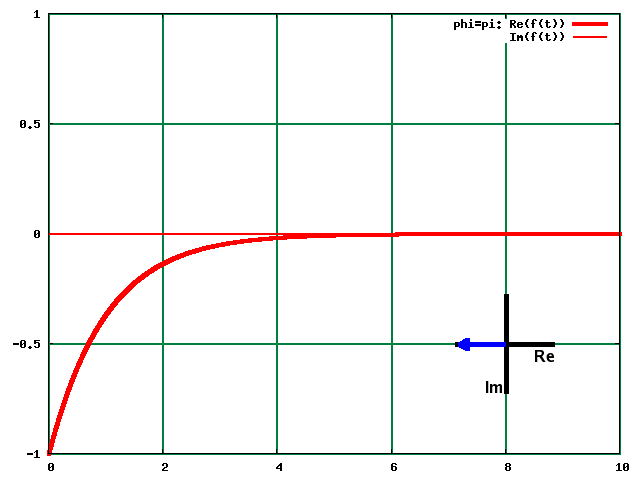
Ar π, mae'r rhan real wedi ei wrthdroi; felly mae'r spectrwm hefyd wedi ei wrthdroi.

Arosodiad darfodiadau araf a chyflym

Swm dau darfodiad:	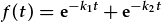$f(t)=e^{-k_1t}+e^{-k_2t}$
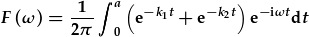transforms as	$F(\omega)=\frac{1}{2\pi}\int_0^a(e^{-k_1t}+e^{-k_2t})e^{-i\omega t}dt$ .
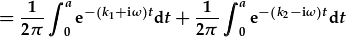
Gellir gwahanu'r integreiddiad:	$=\frac{1}{2\pi}\int_0^ae^{-(k_1+i\omega)t}dt+\frac{1}{2\pi}\int_0^ae^{-(k_2-i\omega)t}dt$
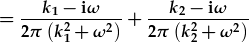i'r ddau ffurf arferol. Felly,	$=\frac{k_1-i\omega}{2\pi(k_1^2+\omega^2)}+\frac{k_2-i\omega}{2\pi(k_2^2+\omega^2)}$ .

Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

Mae hwn yn esiampl o'r damcaneb adiad ar waith.
Mae'r darfodiad cyflym yn cyfrannu cydran spectraidd llydan; mae'r darfodiad araf yn achosi cydran cul. Meddyliwch Fourier!
Yn yr esiampl yma, mae arddwysedd (integreiddiad) y ddau linell yr un fath, er nad yw'n ymddangos felly. Mae hwn yn broblem cyffredin pan yn edrych ar spectymau: mae tueddiad i anwybyddu'r llinellau llydan, enwedig pan fod swn yn eu cuddio.

Osgiliad gwanychol

Y ffordd mwyaf hwylus o ddisgrifio osgiliad yw efo esbonyddion cymhlyg. Mae osgiliad gwanychol yn ddarfodiad esbonyddol (fel o blaen) gyda osgiliad wedi ei arosod, h.y. wedi ei luosi fewn.

Felly, y ffwythiant mewnbwn yw:	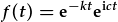$f(t)=e^{-kt}e^{ict}$ ,
sy'n trawsffurfio i:	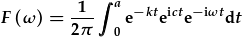$F(\omega)=\frac{1}{2\pi}\int_0^ae^{-kt}e^{ict}e^{-i\omega t}dt$ .
Integreiddio:	$=\frac{1}{2\pi}[-\frac{e^{-(k+i(\omega-c))t}}{k+i(\omega-c)}]_0^a$ ,
amnewid cyfyngau:	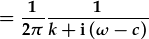$=\frac{1}{2\pi}\frac{1}{k+i(\omega-c)}$ ,
a thacluso	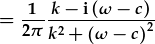$=\frac{1}{2\pi}\frac{k-i(\omega-c)}{k^2+(\omega-c)^2}$ .

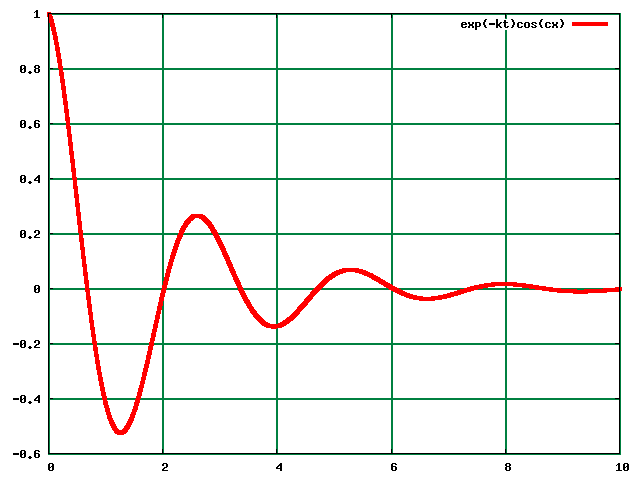Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

Mae'r osgiliad yn achosi'r spectrwm i syfliadu. Mae'r syfliad o safle'r llinell wreiddiol yn hafal i amled yr osgiliad.
Tra bod y darfodiad yn penderfynu lled y llinell, mae'r amled yn penderfynu'r safle. Dyma pan fod trawsffurfiad Fourier mor ddefnyddiol mewn spectroscopeg: O safle'r llinell rydym yn gweld pa amled (a felly egni) mae rhyngweithio'n digwydd, ac o lled y llinell, gallwn ddod i gasgliadau am ystod posib y rhyngweithio. Yn olaf, mae arddwysedd y llinell yn dangos pa mor debygol yw'r trosiant rhwng gwahanol lefelau egni i ddigwydd.
Mae'r gwybodath yma i gyd yn y data parth-amser gwreiddiol, ond mae trawsffurfiad Fourier yn ein helpu i'w ddarllen o'r data gwreiddiol --sydd fel arfer yn fler!

Dau osgiliad

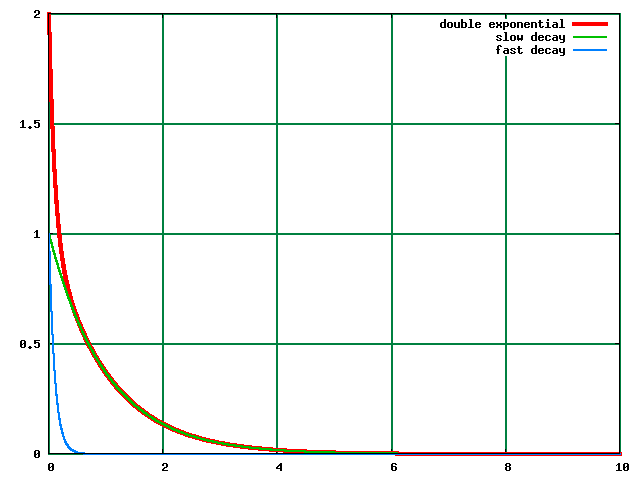
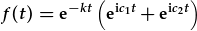Mewn system gyda dau gwahanol trosiant egni, mae ffotonau o dau amledd gwahanol yn cael eu amsugno. Felly mae gennym darfodiad esbonyddol gyda dau amledd arosodol: $f(t)=e^{-kt}(e^{ic_1t)+e^{ic_2t}}$ .

Yn ol y damcaneb adiad, mae hyn yn rhoi dau linell ar wahan, wedi eu syfliadu gan eu amledd, c₁ a c₂, yn ol eu trefn.

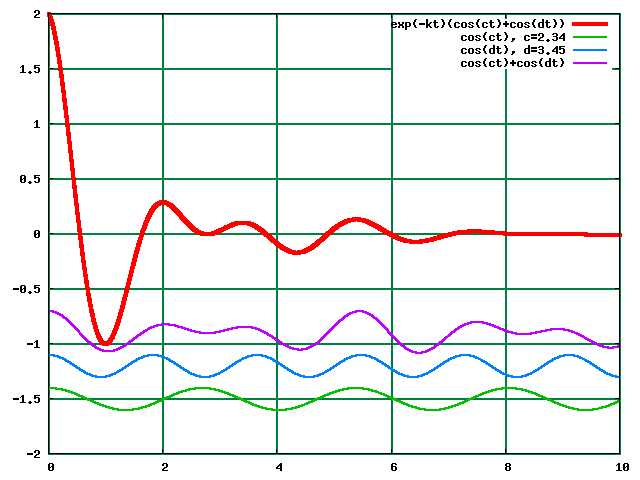Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

Mae'r ffwythiant mewnbwn yn cynnwys dau osgiliad gyda amleddu c₁ a c₂; mae'r ddau osgiliad efo'u gilydd yn ffurfio clystyrau. Hyd yn oed efo dim ond dau osgiliad ac heb swn, mae'r ffwythiant gwreiddiol yn edrych yn eithaf bler.
Mae'r spectrwm yn ymddangos fel un llinell lydan, er fod y crib yn fwy crwn na'r arferol. Drwy plotio'r ddau cydran ar wahan, gallwn weld fod y llinell lydan yn arosodiad o ddau llinell o'r proffil arferol ar yr amleddu addas. Nodwch fod osgled mwyaf y spectrwm ddim ar un o'r amleddu yma, ond rhyngddynt.
Os nad ydym yn gwybod yr amleddu cydranol, gellir dadansoddi'r proffil drwy ffitio cromlinnau.

Cwtogiad: wigladau Fourier

Nid yw setiau data arbrofol yn parhau am byth. Os cwtogir set data cyn i'r holl osgliadau farw, mae hoff elyn y spectrosgebydd, y wigladau Fourier, yn codi ei ben.
Hyd yma, rydym wedi tybio y gallwn orffen yr integreiddiad ar rhyw werth a pryd mae'r signal mwy ne lai ar sero.

Dyma beth sy'n digwydd pan fod y ffwythiant mewnbwn yn syrthio'n ddisymwth i sero, h.y. mae'r set data yn gorffen rhy gynnar.

Lluosi y darfodiad arferol gyda ffwythiant gris:	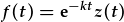$f(t)=e^{-kt}z(t)$ ,
lle	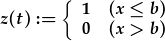$z(t):={1 (x\leq b); 0 (x >b)$ ,
ble mae f(t) mwy ne lai yn sero ar t=b.
Y trawsffurfiad Fourier yw:	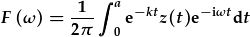$F(\omega)=\frac{1}{2\pi}\int_0^ae^{-kt}z(t)e^{-i\omega t}dt$ ,
ond mae z(t) yn gorfodi f(t)=0 ar t>b:	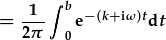$=\frac{1}{2\pi}\int_0^be^{-(k+i\omega)t}dt$ .
Integreiddioe:	$=\frac{1}{2\pi}[-\frac{e^{-(k+i\omega)t}}{k+i\omega}]_0^b$
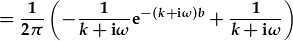
ac amnewid cyfyngau:	$=\frac{1}{2\pi}(-\frac{1}{k+i\omega}e^{-(k+i\omega)b)}+\frac{1}{k+i\omega})$
oherwydd y tro yma, ar t=b, nid yw f(t) wedi darfodi'n llwyr.
Tacluso:	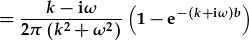$=\frac{k-i\omega}{2\pi(k^2+\omega^2)}(1-e^{-(k+i\omega)b})$ .

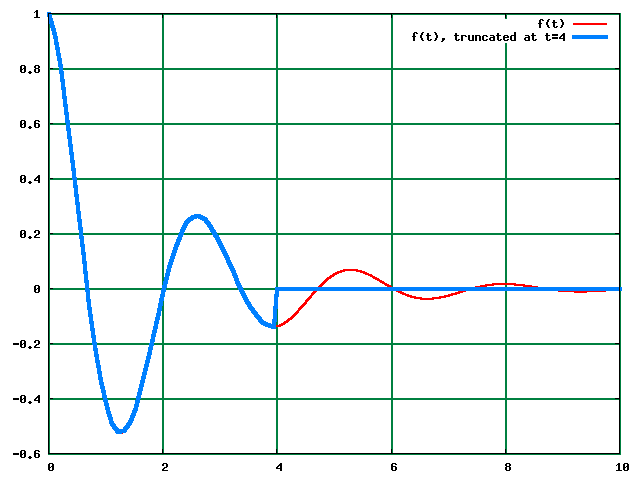Fig.: Truncated function and its Fourier transform.

Cliciwch ar y ddelwedd i drawsffurfio. (Yn arallddewisiol, edrychwch ar y trawsffurfiad yma.)

Mae'r ffwythiant gwreiddiol wedi ei gwtogi ar t=4 yn yr esiampl hwn.
Mae spectrwm y ffwythiant cwtogedig yn dangos wigliadau cyfnodol i bob ochr y prif linell. Mae lluosi y ffwythiant mewnbwn gwreiddiol gyda ffwythiant gris ar ol trawsffurfiad yn gyfrodedd o'r spectrwm gwreiddiol gyda ffwythiant sinx/x (a elwir weithiau yn sincx).
Nid yw'r wigliadau Fourier yn effeithio safle'r llinellau spectraidd, ond maent yn effeithio lled ac arddwysedd y llinell. Os oes nifer o linellau yn bresenol, mae wigliadau Fourier sy'n perthyn i linell cryf yn medru gorgyffwrdd llinell gwan, gan greu syfliad o'r llinell gwan.
Yn ymarferol, yr unig ffordd i osgoi hyn yw gwneud yn siwr fod y data yn cael ei ddarllen am amser digon hir. Os nad yw hyn yn bosibl, gellir lluosi'r data amrwd gan darfodiad esbonyddol sy'n gorfodi'r data lawr i mwy ne lai sero ar ddiwedd y set data. Mae hyn yn lleihau'r wigliadau ond yn cynyddu lled y llinell.

Mae hyn yn gorffen yr adran ar drawsffurfiadau Fourier. Dyma'r daflen waith addas a'i datrysiadau.

Mae yna hefyd taflen gymorth i helpu eich adolygiad.