[English]

Adiadau

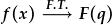Gadewn i f(x)\stackrel{\text{F.T.}}{\longrightarrow}F(q),
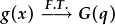a g(x)\stackrel{\text{F.T.}}{\longrightarrow}G(q).
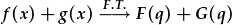Yna f(x)+g(x)\stackrel{\text{F.T.}}{\longrightarrow}F(q)+G(q),

h.y. trawffurfiad Fourier (TF) swm yw'r swm o'r TF unigol, sef beth y byddem wedi tybio ta beth.

Dyma'r prawf:
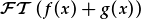FT(f(x)+g(x))=\int(f(x)+g(x))e^{-iqx}dx=\frac{1}{2\pi}\int f(x)e^{iqx}dx+\frac{1}{2\pi}\int g(x)e^{iqx}dx=F(q)+G(q).

Cyfrodedd

Yn anffodus, nid yw lluosi yr un mor syml.
Nodwch fod f(x)\cdot g(x)\stackrel{\text{F.T.}}{XXX}F(q)\cdot G(q)!

Yn hytrach, mae lluoswm dau trawsffurfiad Fourier yn gyfrodedd o'r ddau ffwythiant gwreiddiol:
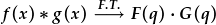f(x)\ast g(x)\stackrel{\text{F.T.}}{\longrightarrow}F(q)\cdot G(q).

Diffinir cyfrodedd f(x) a g(x) fel 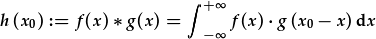h(x_0):=f(x)\ast g(x)=\int_{-\infty}^{+\infty}f(x)\cdot g(x_0-x)dx, h.y. mae gwerth y cyfrodedd yn cael ei gyfrifo i bob pwynt x0 yn eu tro drwy integreddio gyda pherthynas i x. Mae'r integreiddiad yn lluoswm o un o'r ffwythiannau ar x a'r ffwythiant arall dros y pellter rhwng x a'r gwerth penodol o x0 lle mae'r cyfrodedd i'w gyfrifo.

I ddychmygu'r ffurf hwn, meddyliwch am ddau linell spectraidd sy'n gorgyffwrdd: Os yw'r ddau linell yn bell o'u gilydd, does bron dim gorgyffwrdd. I'r gwrthwyneb, os yw'r ddau linell yn agos, mae'r gorgyffwrdd yn cynyddu. Mae maint y gorgyffwrdd, fel y gellir gweld o linell 1, yn dibynnu ar osgled llinell 1 ei hun a'r pellter rhwng llinell 1 a 2.

Syfliadau

Mae trawsffurfiadau Fourier wedi eu seilio ar arosodiad o ffwythiannau cyfnodol. Pan yn syfliadu ystod ffwythiant cyfnodol ar yr echel x, rydym yn newid cydwedd y don sin. Yn sgil hyn, rhaid cynnwys ffactor cydwedd (esbonydd cymhlyg) yn y trawsffurfiad Fourier:

Unwaith eto, gadewn i 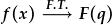f(x)\stackrel{\text{F.T.}}{\longrightarrow}F(q).
I benderfynu TF y ffwythiant wedi ei syfliadu gan a: 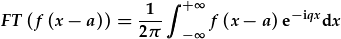FT(f(x-a))=\frac{1}{2\pi}\int_{-\infty}^{+\infty}f(x-a)e^{-iqx}dx.
Gorfodi (x-a) i ymddangos yn yr esbonydd: 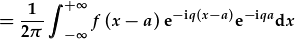=\frac{1}{2\pi}\int_{-\infty}^{+\infty}f(x-a)e^{-iq(x-a)}e^{-iqa}dx.

Pe bae'r differiad yn d(x-a) yn hytrach na dx, byddai'r integriad yn cynnwys trawsffurfiad Fourier f(x-a). I wireddu hyn, rhaid i ni syfliadu cyfwng yr integreiddiad.

I gyfrifo hyn, cysudrwch y swm 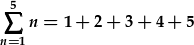\sum_{n=1}^{5}n=1+2+3+4+5.
Mae hwn yr un fath a'r swm 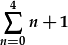\sum_{n=0}^{4}n+1,
neu hyd yn oed 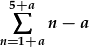\sum_{n=1+a}^{5+a}n-a.

Gallwn syfliadu'r cyfwng ag a os rydym yn cydbwyso hyn gyda fformiwla y swm.
Mae'r un tric yn gweithio gyda integreiddion oherwydd analog parahaol swm yw integreiddiad.

Er mwyn amnewid dx gyda d(x-a), mae rhaid i ni syfliadu y cyfyngau integreiddio is ac uwch drwy +a.

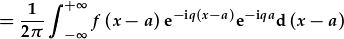Yn lwcus, mae swm anfeidredd ac a yn aros yn anfeidredd, felly does dim gwahaniaeth: =\frac{1}{2\pi}\int_{-\infty}^{+\infty}f(x-a)e^{-iq(x-a)}e^{-iqa}d(x-a).
Felly, 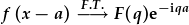f(x-a)\stackrel{\text{F.T.}}{\longrightarrow}F(q)e^{-jqa}.

I gloi'r adran Furier yma, gwnawn ychydig o drawsffurfio ymarferol.