[English]

Y stori hyd yn hyn...

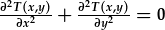
Mae gennym wedi ei wahanu \frac{\parti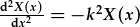a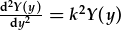l^2T(x,y)}{\partial x^2}+\frac{\partial^2T(x,y)}{\partial y^2}=0
i \frac{d^2X(x)}{dx^2}=-k^2X(x) a \frac{d^2Y(y)}{dy^2}=k^2Y(y),
lle k2 yw'r cysonyn gwahanu.
Rhain yw'r HDC gyda cyfernodau cyson
gyda'r cysonion: $a_2=1$; $a_1=0$; $a_0=-k^2$ a $a_2=1$; $a_1=0$; $a_0=k^2$.
Felly, yr israddau yw: $$k_{1,2}=-0\pm\sqrt{0+\frac{k^2}{1}}=\pm k$$ and $$k_{1,2}=-0\pm\sqrt{0-\frac{k^2}{1}}=\pm ik$$,
lle i yw'r uned cymhlyg. Datrysiadau y ddau HDC gradd 1af yw
cyfuniadau llinol o'r ddau isradd: $$X(x)=c_1e^{kx}+c_2e^{-kx}$$ a $$Y(y)=c_1e^{iky}+c_2e^{-iky}$$.

Gan gyfuno'r datrysiadau rhannol

Gan gofio fod esbonydd real yn ffwythiant sy'n cynyddu neu gostwng yn fonotonig tra bod esbonydd cymhlyg yn ffwythiant sy'n osileiddio: 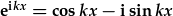e^{ikx}=\cos{kx}-i\sin{kx}, datrysiadau posibl (mathemategol) hafaliad Laplace yw

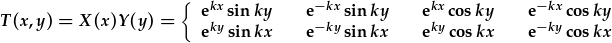
T(x,y)=X(x)Y(y)={e^{kx}\sin{ky};e^{-kx}\sin{ky};e^{kx}\cos{ky};e^{-kx}\cos{ky};e^{ky}\sin{kx};e^{-ky}\sin{kx};e^{ky}\cos{kx};e^{-ky}\cos{kx}}

neu unrhyw gyfuniad llinol o'r uchod.

Amodau terfyn yr esiampl plat poeth

Nid yw gyd o'r datrysiadau mathemategol yn gwneud synhwyr ffisegol. Mae'r amodau terfyn yn penderfynu'r datrysiadau synhwyrol o'r broblem ffisegol

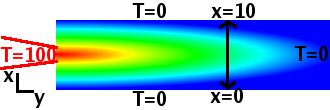
Fig.: Plat hir wedi ei gynhesu ar un ochr tra bod yr ochrau eraill yn oer.

Yr amodau terfyn yn yr esiampl yma yw:

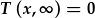T(x,\infty)=0 (de)
T(0,y)=0 (gwaelod)
T(10,y)=0 (top)
T(x,0)=100 (chwith)

Mae'r amod gyntaf, 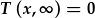T(x,\infty)=0, yn diddymu'r holl datrysiadau sy'n osileiddio ar hyd yr echel y gan fod proffil y tymheredd yn syrthio'n fonotonig o'r chwith i'r dde. Mae hwn yn diddymu 4 o'r 8 datrysiad:

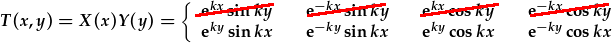
T(x,y)=X(x)Y(y)=e^{ky}\sin{kx};e^{-ky}\sin{kx};e^{ky}\cos{kx};e^{-ky}\cos{kx}}

Mae'r un amod terfyn hefyd yn gwrthddweud datrysiadau sy'n cynyddu yn hytrach na syrthio ar hyd yr echel y, h.y. yr esbonyddion posotif. Felly, dyna diddymu dau arall:

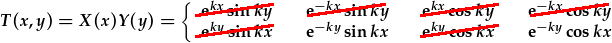
T(x,y)=X(x)Y(y)=e^{-ky}\sin{kx};e^{-ky}\cos{kx}}

Mae'r ail amod terfyn, T(0,y)=0, yn gofyn am ffwythiant osileiddaidd ar x sy'n sero ar x=0. Yn sgil hyn, o'r ddau datrysiad sy'n weddill, gallwn diddymu'r un a thermau cosin:

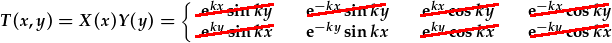
T(x,y)=X(x)Y(y)=e^{-ky}\sin{kx}

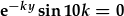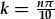Gallwn nawr defnyddio'r trydydd amod terfyn, T(10,y)=0, i rhoi cyfyngiadau ar y cysonyn k. Gan osod yr AT i'r datrysiad cyffredinol cywir, cawn e^{-ky}\sin{10k}=0. Mae'r ochr chwith yn hafal i sero os yw unrhyw un o'r ffactorau yn sero. Mae'r esbonydd yn sero pan mae y yn cyrraedd anfeidredd; israddau y ffactor sin yw k=\frac{n\pi}{10}, lle gall n fod yn unrhyw integer.

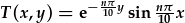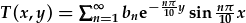Felly, rhaid fod ffurf T(x,y)=e^{-\frac{n\pi}{10}y}\sin{\frac{n\pi}{10}x} i'r datrysiad ffisegol, neu unrhyw gyfuniad llinol o'r fath dermau. Mae cyfuniad llinol o'r holl termau posibl gydag n=1,2,3,... (gyda cyfernodau llinol bn) yn T(x,y)=\sum_{n=1}^{\infty}b_ne^{-\frac{n\pi}{10}y}\sin{\frac{n\pi}{10}x}. Mae hwn yn gyfres sin Fourier , a gallwn ffeindio'r cyfernodau drwy cymhwyso'r amod terfyn olaf ac integreiddio.

I barhau gyda datrysiad hafaliad Laplace, rhaid cyntaf darganfod syt i gyfrifo'r cyfernodau Fourier.