Mae angen amodau terfynol (AT) ar gyfer dewis y datrysiad ffisegol addas neu datrysiad o'r amrywiad mwy eang o'r rhai sy'n gywir yn fathemategol. Yn yr esiampl o ddarfodiad ymbelydrol yn gynharach, roedd yna nifer anfeidrol o ddatrysiadau mathemategol cywir (pob un a cyfernodau gwahanol a0). Mewn cyd-destun ffisegol arbennig, byddwn yn dewis yn gall datrysiad lle fod y cyfernod yn hafal i'r nifer cychwynnol o atomau ymbelydrol
Dyma esiampl arall: Beth yw'r pellter, x, mae gwrthrych yn syrthio dan ddylanwad disgyrchiant mewn amser t? Gofal - x yw'r newidyn dibynnol yma; x(t)!
| Nodiant ffysegol | Nodiant rhywogaethol | |||
|---|---|---|---|---|
| pellter syrthio: | x | - | newidyn dib.: | y |
| amser: | t | - | newidyn annib.: | x |
| cyflymiad oherwydd disgyrchiant: | g | - | cyfernod: | c |
| HDC i'w ddatrys: | 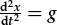 |
- | 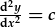 |
|
| Integreiddiwch: | 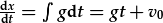 |
- | 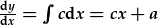 |
|
| ac integreiddiwch eto: | 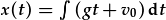 |
- | 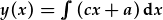 |
|
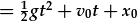 |
- | 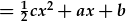 |
||
Mae'r camau integreiddio yn creu cysonyn integreiddio (v0 a x0 neu a a b yn yr esiampl hwn). Mae'r cysonyn v0 yn cael ei adio i gt (unedau ms-2·s); felly mae'n rhaid mai cyflymder yw. Mae'r cysonyn x0 yn cael ei adio i gt2 (unedau ms-2·s2); felly hyd yw. Gan ein bod yn datrys ar gyfer safle fel ffwythiant amswer, x(t), mae'n synhwyrol i adnabod y cysonion hyn fel y cyflymder a safle yn y cychwyn, h.y. x0=x(t=0) a v0=v(t=0). Mae amodau terfynnol sy'n cyfateb i bwynt mewn amser yn cael eu galwn weithiau'n amodau cychwynnol.
Mae pob amod terfynol mewn gwirionedd yn gysonyn integreiddio.
-> Mae pob cam integreiddio yn codi'r angen am un amod terfynol.
-> I ddatrys HDC o radd n, rhaid darparu n amod terfynol.
Ar gyfer HDC, mae'n ddigonol cael yr un nifer o AT a'r swm o'r graddau gyda pherthynas i'r holl newidion annibynnol. Fodd bynnag, weithiau nid oes angen gymaint. Mae hyn yn digwydd pan fod modd integreddio gyda pherthynas i wahanol newidion mewn un cam fel fod modd cyfuno'r TA yn un.
Nesa, trwon at HDC a'u defnydd yn ffiseg.