Trawsffurfiad Fourier 1 - cyflwyniad :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

Esbonyddion cymhlyg yn ffwythiannau cyfnodol

Gellir mynegi sinau a cosinau real fel esbonyddion cymhlyg:
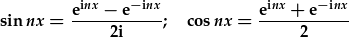
$\sin{nx}=\frac{e^{inx}-e^{-inx}}{2i};\cos{nx}=\frac{e^{inx}+e^{-inx}}{2}$
Mae nifer o brosesau ffisegol yn gyfnodol a gellir eu trin fel cyfuniad o ffwythiannau sin neu cosin. Yn ychwanegol, rydym wedi gweld fod modd ehangu nifer o ffwythiannau, hyd yn oed rhai anghyfnodol, fewn i gyfres Fourier, h.y. cyfres o harmoniau sin neu cosin (neu, yn fwy cyffredinol, ffwythiannau esbonyddol cymhlyg).

Cyfernodau Fourier

Yn y gyfres sin real pur,	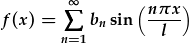$f(x)=\sum_{n=1}^{\infty}b_n\sin{\frac{n\pi x}{l}}$ ,
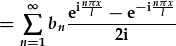
amnewid y sin gyda esbonyddion cymhlyg:	$=\sum_{n=1}^{\infty}b_n\frac{e^{i\frac{n\pi x}{l}}-e^{-i\frac{n\pi x}{l}}}{2i}$
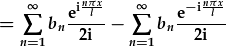a hollti'r swm:	$=\sum_{n=1}^{\infty}b_n\frac{e^{i\frac{n\pi x}{l}}}{2i}-\sum_{n=1}^{\infty}b_n\frac{e^{-i\frac{n\pi x}{l}}}{2i}$ .
Mae swm yr -n o 1 i anfeidredd yr un fath a'r swm o +n o -anfeidredd i -1.
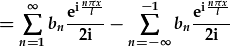Felly, gallwn gyfri'r ail swm ar i nol:	$=\sum_{n=1}^{\infty}b_n\frac{e^{i\frac{n\pi x}{l}}}{2i}-\sum_{n=-\infty}^{-1}b_n\frac{e^{i\frac{n\pi x}{l}}}{2i}$ .
Gan fod y ddau swm yr un fath, gallwn eu cyfuno:	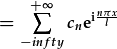$=\sum_{-infty}^{+\infty}c_ne^{i\frac{n\pi x}{l}}$ ,
ble	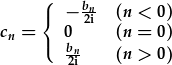$c_n={-\frac{b_n}{2i}(n\lt 0);0(n=0);\frac{b_n}{2i}(n />0)$

Nodwch fod i'r cyfres sin pur, c₀=0, ond yn gyffredinol (cyfresi cosin neu cymysg) nid hyn yw'r achos. Yn gyffredinol,

ffeindir y c_n drwy	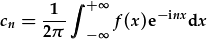$c_n=\frac{1}{2\pi}\int_{-\infty}^{+\infty}f(x)e^{-inx}dx$
i ehangu	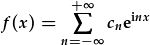$f(x)=\sum_{n=-\infty}^{+\infty}c_ne^{inx}$ .

Cyfres Fourier arwahanol a trawsffurfiad Fourier parhaol

Felly, rydym angen datrys integriad i ffeindio cyfernodau yn y gyfres Fourier. Mae'r mynegrifau yn y gyfres ac o fewn yr integriad yr un fath heblaw am yr arwydd. Gallwn cymryd mantais o'r cymesuredd yma i symud o gyfres Fourier arwahanol i drawsffurfiad Fourier parhaol:

arwahanol	->	parhaol
newidyn indecs n	->	newidyn parhaol q
cyfernodau Fourier c_n	->	trawsffurfiad Fourier g(q)
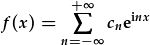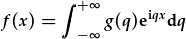$f(x)=\sum_{n=-\infty}^{+\infty}c_ne^{inx}$	->	$f(x)=\int_{-\infty}^{+\infty}g(q)e^{iqx}dq$
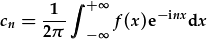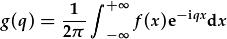$c_n=\frac{1}{2\pi}\int_{-\infty}^{+\infty}f(x)e^{-inx}dx$	->	$g(q)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}f(x)e^{-iqx}dx$

Newidir y set o gyfernodau c_n sy'n dibynnu ar newidyn indecs arwahanol n gan ffwythiant parhaol g(q), yn dibynnu ar newidyn parhaol q.
g(q) yw'r trawsffurfiad Fourier o f(x); f(x) yw'r trawsffurfiad Fourier gwrthdroedig o g(q). Nodwch y cymesuredd!

Parau Fourier yn ffiseg

Oherwydd cymesuredd y trawsffurfiad Fourier a'r trawsffurfiad Fourier gwrthdroedig, mae nifer o rhinweddau ffisegol yn dod mewn parau Fourier: os ydych yn mesur un, rydych yn derbyn y llall drwy drawsffurfiad Fourier. Mae hwn yn dechneg hynod o ddefnyddiol, ac yn gyffredin iawn mewn ffiseg arbrofol. Y ddau esiampl cyffredin yw technegau spectroscopaidd a gwasgariad:

Spectrosopi: Amser ac amledd
Mae trawsnewid rhwng lefelau egni (e.e. gwahanol stad dirgrynnu moleciwlar neu stadau cynyrfedig electron mewn lled-ddargludyddion etc.) yn gofyn am maint penodol o egni, sy'n cael ei ddarparu gan ffoton o'r amledd cyfatebol. Er hyn, mae'n aml yn haws i ymbelydru'r sampl gan tardd gwyn (h.y. tardd o olau sy'n cynnwys gyd o'r amleddau dros ystod sy'n cynnwys y band addas) a mesur ymateb y sampl fel ffwythiant o amser. Mae hyn yn arbed yr ymdrech o ffeindio tardd monogromatig, ac yn gyflymach. 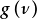Mae trawsnewid Fourier y signal f(t) sy'n cael ei fesur fel ffwythiant o amser t yn datgelu y spectrwm amledd $g(\nu)$ o'r system.
Gwasgaru: Gofod a gofod cilyddol
Pan diffreithir ffotonau gan plan latis o gristal, mae ymyrraeth positif o ganlyniad i wasgaru gan atomau gwahanol mewn lleoliadau cymesureddol yn cynhyrchu macsima o arddwysedd gwasgaru ar rhai onglau gyda pherthynas i'r pelydr mewnbynol. Mae pigau Bragg o'r fath yn ymddangos ar onglau mawr os yw'r gwasgarwyr yn agos i'w gilydd, ac ar onglau bach os ydynt yn bell: mae diffreithiant yn mapio gofod cilyddol. I alluogi ffeindio gwybodaeth o'r gofod real, h.y. safle'r atomau, rhaid gwneud trawsffurfiad Fourier o'r patrwm gwasgaru. Mae'r trawsffurfiad Fourier g(r) yn cynnwys yr un gwybodaeth a'r patrwm gwreiddiol f(q); felly mae'n arferol dangos patrymau diffreithiant yng ngofod cilyddol. Er hyn, mae'n haws cyfrifo'r rhifau cyfesurynol (y rhif o gymdogion) atomig mewn gofod real, ac yn yr achos yma defnyddir trawsffurfiad Fourier.

Gallwn nawr edrych ar rhai damcanebion Fourier a gweld syt i rhagdybio ymddangosiad trawsffurfiad Fourier heb orfod gwneud y mathemateg llawn.