Y gweithredydd del :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

Llethrau mewn un dimensiwn

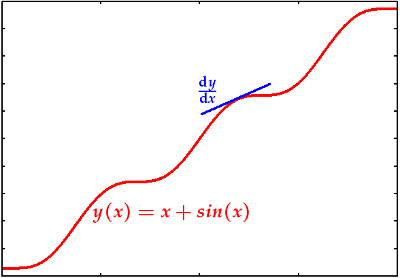
Fig.: y(x) a'r tangiad i'r llethr dy/dx ar un pwynt penodol.

Mae'n arferol efo ffwythiant y(x) mewn un dimensiwn (h.y. un sydd a ond un newidyn annibynnol, yn yr achos yma x) i plotio'r newidyn annibynnol ar yr absisa a'r y(x) ar y mesuryn. Yn y gynrhychioliaeth yma, y differydd dy/dx yw'r ffwythiant sy'n cynrhychioli y llethr i'r tangiad i y(x) pan mae x yn newid.

Nodwch mai nid y tangiad ei hun ond gwerth ei lethr fel ffwythiant o x a ddangosir.

Llethrau mewn dau dimensiwn

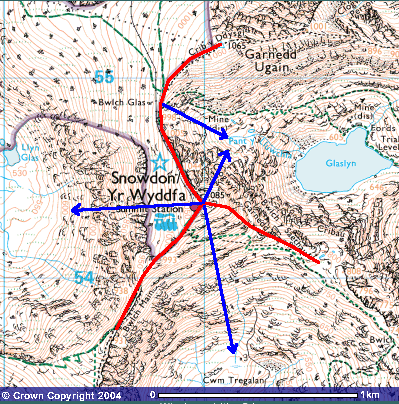Fig.: Map AO o'r Wyddfa yn dangos cribau a graddiannau.

Delwedd wedi ei gynhyrchu o wasanaeth Get-a-map yr Arolwg Ordnans. Dangosir y ddelwedd gyda chaniatad caredig yr Arolwg Ordnans ac Arolwg Ordnans Gogledd Iwerddon.

Gellir plotio ffwythiant dau ddimensiwn z(x,y) trwy cynrhychioli gwerthoedd y ffwythiant gyda wahanol lliwiau neu gyda llinellau cromlin, gyda'r ddau newidion annibynnol x a y ar y ddwy echel. Mae map arolwg ordnans yn plotio uchder uwchben lefel y mor fel ffwythiant o'r ddau newidion annibynnol lledredd a hydred.

I gyrraedd copa mynydd, gallwch innau cerdded lan y cribau (llinellau coch) neu dringo'r clogwyni yng nghefn y dyffrynoedd (llinellau glas).

O gopa'r Wyddfa, nid yw'r llethr 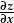$\frac{\partial z}{\partial x}$ (dwyrain-gorllewin), na'r llethr 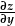$\frac{\partial z}{\partial y}$ (gogledd-de) yn dilyn y llethr mwyaf serth i lawr. Mae'r graddiant mwyaf serth o'r copa yn dilyn llinell gogledd-gogledd ddwyrain fewn i Cwm Glaslyn.

Y graddiant yw'r llethr mwyaf serth i unrhyw bwynt, nid dim ond ar y copa. Gan ein bod angen gwybod pa mor serth yw'r llethr, a'r cyfeiriad mae'n gwynebu, mae'n rhinwedd fector.

Y gweithredydd del

Diffinir gweithredydd fector 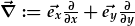$\vec{\nabla}:=\vec{e_x}\frac{\partial}{\partial x}+\vec{e_y}\frac{\partial}{\partial y}$ . Hwn yw'r gweithredydd del (neu'r gweithreydd Nabla) mewn dau dimensiwn. Mae'n rhwydd adio termau cyfatebol i dimensiwnau uwch os oes angen.

Gellir defnyddio'r gweithredydd del ar

ffwythiant scalar:

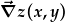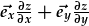
$\vec{\nabla}z(x,y)$	=	$\vec{e_x}\frac{\partial z}{\partial x}+\vec{e_y}\frac{\partial z}{\partial y}$
Mae hyn yn cynhyrchu gwerthoedd arwahan i'r dau differydd ar bob pwynt yng ngofod x,y:	=	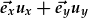$\vec{e_x}u_x+\vec{e_y}u_y$ ,
a gellir ei ysgrifennu fel fector:	=	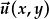$\vec{u}(x,y)$ .

Mae'r ffwythiant fector efo cydrannau x a y i bob pwynt yng ngofod x,y.
Gelwir y ffwythiant fector yma yn graddiant y ffwythiant scalar gwreiddiol. Yn y modd hwn, mae maes trydanol yn raddiant i'r potensial trydanol.

ffwythiant fector:

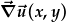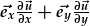
$\vec{\nabla}\vec{u}(x,y)$	=	$\vec{e_x}\frac{\partial\vec{u}}{\partial x}+\vec{e_y}\frac{\partial\vec{u}}{\partial y}$
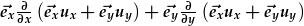Mae'r differynnau yn gweithredu ar wahan i bob cydran:	=	$\vec{e_x}\frac{\partial}{\partial x}(\vec{e_x}u_x+\vec{e_y}u_y)+\vec{e_y}\frac{\partial}{\partial y}(\vec{e_x}u_x+\vec{e_y}u_y)$ .
Mae'r fectorau unedol yn orthogonol:	=	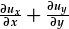$\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}$ ,
sy'n arwain at ffwythiant scalar:	=	f(x,y).

Adnabyddir y ffwythiant scalar f(x,y) fel dargyfeiredd y ffwythiant fector gwreiddiol.

Felly, mae'r gweithredydd del yn troi ffwythiannau scalar fewn i ffwythiannau fector a ffwythiannau fector fewn i ffwythiannau scalar. Os gweithredir dwy waith ar ffwythiannau scalar, y canlyniad yw ffwythiant scalar arall: 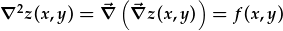$\nabla^2z(x,y)=\vec{\nabla}(\vec{\nabla}z(x,y))=f(x,y)$ . Hwn yw 2il differyn z(x,y) ar y llethr mwyaf serth.

Dargyfeiredd a cwrl

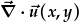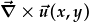Mae'r dargyfeiredd, $\vec{\nabla}\cdot\vec{u}(x,y)$ , yn weithredydd sy'n gyfwerth a lluoswm scalar dau fector. Mae analog y lluoswm fector, $\vec{\nabla}\times\vec{u}(x,y)$ , yn bodoli yn ogystal. Fe'i elwir yn cwrl gan ei fod yn mesur camedd ffwythiannau.

Y gweithredydd del mewn cyfesurynnau pegynol

Mewn cyfesur Cartesiaidd, mae'r gweithredydd del a'r un ffurf pan yn gweithredu ar ffwythiannau scalar scalar neu fector. Nid dyma'r achos mewn cyfesurynnau pegynol (sfferaidd neu silindraidd).

Wedi atgoffa'n hun o fel mae'r gweithredydd del yn gweithio, gallwn ddatrys hafaliad Laplace a HDC 2il radd eraill.