HDC llinol o unrhyw radd gyda cyfernodau cyson :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

Ail radd

I ddatrys HDC ail radd gyda cyfernodau cyson:	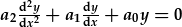$a_2\frac{d^2y}{dx^2}+a_1\frac{dy}{dx}+a_0y=0$ ,
rhannwch gyda'r cyfernodyn gradd uchaf:	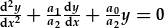$\frac{d^2y}{dx^2}+\frac{a_1}{a_2}\frac{dy}{dx}+\frac{a_0}{a_2}y=0$ ,
a ffactorwch i ddiddymu'r y	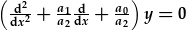$(\frac{d^2}{dx^2}+\frac{a_1}{a_2}\frac{d}{dx}+\frac{a_0}{a_2})y=0$ ,

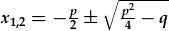Mae'r ochr chwith yn sero os yw y=0, sydd ddim yn wir fel rheol gan mae'r neidyn dibynnol yw, neu os yw'r mynegiad yn y bracedi yn sero. Mae ffeindio israddau or mynegiad braced yn gyfatebol i datrys hafaliad polinomaidd o'r ail radd: Mae israddau yr hafaliad x²+px+q=0, sy'n ffactoredig fel (x+x₁)(x+x₂)=0, yn $x_{1,2}=\frac{p}{2}\pm\sqrt{\frac{p^2}{4}-q}$ .

Yn yr un modd, israddau	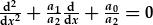$\frac{d^2}{dx^2}+\frac{a_1}{a_2}\frac{d}{dx}+\frac{a_0}{a_2}=0$
yw	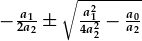$-\frac{a_1}{2a_2}\pm\sqrt{\frac{a_1^2}{4a_2^2}-\frac{a_0}{a_2}}$ .
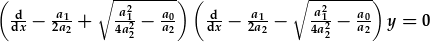Mae'r HDC felly'n	$(\frac{d}{dx}-\frac{a_1}{2a_2}+\sqrt{\frac{a_1^2}{4a_2^2}-\frac{a_0}{a_2}})(\frac{d}{dx}-\frac{a_1}{2a_2}-\sqrt{\frac{a_1^2}{4a_2^2}-\frac{a_0}{a_2}})y=0$ ,
neu trwy ailenwi'r cysonion,	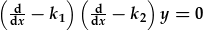$(\frac{d}{dx}-k_1)(\frac{d}{dx}-k_2)y=0$ ,
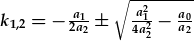lle	$k_{1,2}=\frac{a_1}{2a_2}\pm\sqrt{\frac{a_1^2}{4a_2^2}-\frac{a_0}{a_2}}$ .

Er nad yw gweithredyddion fel rheol yn gymudol, yn yr achos yma nid yw'r drefn mae'r dau gweithredydd (termau bracedi) yn cael eu gweithredu ar y yn bwysig oherwydd dim ond ffactor cyson sy'n wahanol rhyngddynt, a nid yw hyn yn effeithio'r differiant. Dyna pam fod y dechneg angen cyfernodau cyson: Os fyddent yn ffwythiannau x, ni fyddai'r dau weithredydd yn gymudol, a ni fyddai yna gyfatebiaeth gyda hafaliadau polinomial. Gan nad oes ots ar drefn gweithredu'r dau gweithredydd, gallwn rhannu'r hafaliad 2il radd mewn i dau hafaliad gradd 1af sydd modd eu gwahanu:

Gweithredydd cyntaf:	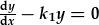$\frac{dy}{dx}-k_1y=0$ ,	a'r ail weithredydd:	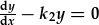$\frac{dy}{dx}-k_2y=0$ .
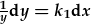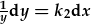Gwahanu:	$\frac{1}{y}dy=k_1dx$	-	$\frac{1}{y}dy=k_2dx$ ,
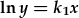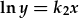integreiddio:	$\ln{y}=k_1x$	-	$\ln{y}=k_2x$ ,
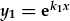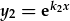a datrys ar gyfer y:	$y_1=e^{k_1x}$	-	$y_2=e^{k_2x}$ .

Datrysiad cyffredinol y HDC gwreiddiol:	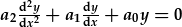$a_2\frac{d^2y}{dx^2}+a_1\frac{dy}{dx}+a_0y=0$
yw unrhyw cyfuniad llinol o'r ddau:	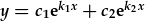$y=c_1e^{k_1x}+c_2e^{k_2x}$ ,
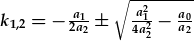where	$k_{1,2}=\frac{a_1}{2a_2}\pm\sqrt{\frac{a_1^2}{4a_2^2}-\frac{a_0}{a_2}}$ .

Nodwch gall k_1,2 fod yn gymhlyg.

Graddau uwch

Gellir datrys HDC llinol gyda cyfernodau cyson o graddau uwch drwy'r egwyddor canlynol. Mae'r nifer o HDC gradd 1af i'w datrys yn hafal i gradd yr hafaliad gwreiddiol. Ffeindir y cysonion cyfatebol k_1,2,3,... drwy ffeindio israddau y polinomial ategol cyfatebol.

Gyda'r gwybodaeth yma, gallwn ddychwelyd i ddatrys hafaliad Laplace.

Ar y pwnt hwn, gallwch geisio yr ail daflen waith. Gwiriwch eich datrysiadau wedi i chi orffen.