Hafaliad trylediad :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

Mae'r hafaliad trylediad yn cysylltu newidiadau mewn gofod gyda newidiadau mewn amser. Mae ganddo deilliadau gofodol ail radd ac un amserol gradd cyntaf. Byddwn yn gweithio ar y datrysiadau cyffredinol yma; mae'r datrysiadau penodol yn dibynnu ar amodau terfun megys y crynodiad ar y dechrau a'r cyfrenodau trylediad. Mae'n defnyddio ehangiad cyfres Fourier fel gyda hafaliad Laplace.

Gwahanu'r newidion

Yr hafaliad trylediad yw:	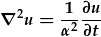$\nabla^2u=\frac{1}{\alpha^2}\frac{\partial u}{\partial t}$ .
Gan dybio datrysiad lluoswm:	u(x,y,t)=F(x,y)·T(t).
Nid yw T(t) yn dibynnu ar x neu y, nid yw F(x,y) yn dibynnu ar t.
Felly gallwn eu cymryd allan o'r deilliadau cyfatebol:	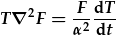$T\nabla^2F=\frac{F}{\alpha^2}\frac{dT}{dt}$ .
Gwahanu termau a cyflwyno cysonyn gwahanu:	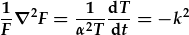$\frac{1}{F}\nabla^2F=\frac{1}{\alpha^2T}\frac{dT}{dt}=-k^2$ .
Y ddadl eto yw, gan fod yr ochr chwith yn annibynnol o amser, a fod yr ochr dde yn annibynnol o cyfesurynnau gofodol, gall y ddau yn gyffredinol ond eu cyfri'n hafal os ydynt yn gyson.
Mae hyn yn ein gadael gyda dau hafaliad ar wahan, un gofodol:	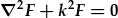$\nabla^2F+k^2F=0$
ac un amserol:	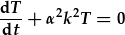$\frac{dT}{dt}+\alpha^2k^2T=0$ .

Nodwch fod y rhan gofodol yn HDR ac yn dibynnu ar x and y!

Rhan amserol

Mae'r rhan amserol yn HDC llinol gradd gyntaf gwahaniaethol. Mae hynny'n hawdd.

Gwahanu newidyn dibynnol ac annibynnol:	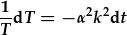$\frac{1}{T}dT=-\alpha^2 k^2dt$ ,
integreiddio:	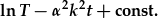$\ln{T}-\alpha^2 k^2t+const.$ ,
a codi i pwer e:	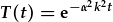$T(t)=e^{-\alpha^2 k^2t}$

(heb amod terfyn ffisegol, gallwn ddewsi cysonyn=0).

Gwahanu eto

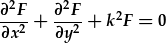
Y rhan gofodol:	$\frac{\partial^2F}{\partial x^2}+\frac{\partial^2F}{\partial y^2}+k^2F=0$
gellir ei wahanu eto:	F(x,y)=X(x)·Y(y).
Amnewid y lluoswm:	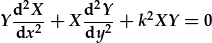$Y\frac{d^2X}{dx^2}+X\frac{d^2Y}{d^2}+k^2XY=0$ ,
gwahanu termau x a y:	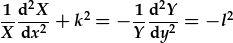$\frac{1}{X}\frac{d^2X}{dx^2}+k^2=-\frac{1}{Y}\frac{d^2Y}{dy^2}=-l^2$ .

Mae'r cysonyn k² yn cael ei rhoi fel rhan o'r term x yn fympwyol. Mae'r ail gwahaniad newidion yn arwain i gysonyn gwahanu arall, l². Yn dilyn y gwahaniad, mae gennym

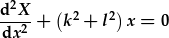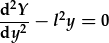two HDC ail radd gyda cyfrenodau cyson:	$\frac{d^2X}{dx^2}+(k^2+l^2)x=0$ ,	$\frac{d^2Y}{dy^2}-l^2y=0$ .
Y cyfernodau ail radd yw:	a₂=1,	a₂=1,
y cyfernodau gradd cyntaf yw:	a₁=0,	a₁=0,
a'r cyfernodau gradd sero yw:	a₀=(k²+l²),	a₀=-l².
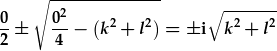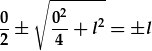Israddau'r polinomial rhinweddol yw:	$\frac{0}{2}\pm\sqrt{\frac{0^2}{4}-(k^2+l^2)}=\pm i\sqrt{k^2+l^2}$ ,	$\frac{0}{2}\pm\sqrt{\frac{0^2}{4}+l^2}=\pm l$ ,
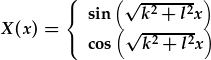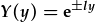a'r datrysiadau yw:	$X(x)=e^{\pm i(k^2+l^2)x}={\sin{(\sqrt{k^2+l^2}x)};\cos{(\sqrt{k^2+l^2}x)}}$ ,	$Y(y)=e^{\pm ly}$ .

Gan rhoi'r datrysiad cyffredinol at ei gilydd

Yn olaf, mae rhaid rhoi'r tri datrysiad rhannol at ei gilydd. Felly'r datrysiadau cyffredinol i'r hafaliad trylediad --gan gofio'r cymesuredd gyda pherthynas i x a y -- yw:

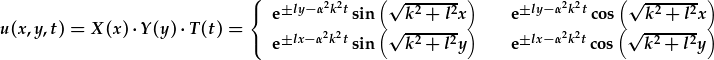$u(x,y,t)=X(x)\cdot Y(y)\cdot T(t)={e^{\pm ly-\alpha^2 k^2t}\sin(\sqrt{k^2+l^2}x);e^{\pm ly-\alpha^2 k^2t}\cos(\sqrt{k^2+l^2}x);e^{\pm lx-\alpha^2 k^2t}\sin(\sqrt{k^2+l^2}y);e^{\pm lx-\alpha^2 k^2t}\cos(\sqrt{k^2+l^2}y)}$ .

Mae taflen waith 3 yn cynnwys esiampl gyda amodau terfyn. Ar ol ei orffen, gwyriwch eich datrysiadau.

Y math cyffredin olaf ar y rhestr o HDR yn ffiseg yw'r hafaliad don.