[English]

Cyfres Fourier sin, cosin a chymhlyg

Defnyddir cyfres Fourier i frasamcanu ffwythiannau anghyfnodol drwy cyfuniad llinol o ffwythiannau cyfnodol. Yn ymarferol, mae mwy a mwy o harmoniau yn cael eu adio nes ceir proffil agos i'r ffwythiant anghyfnodol gwreiddiol.

cyfres fformiwla defnyddir
cyfres sin Fourier 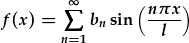f(x)=\sum_{n=1}^{\infty}b_n\sin{\frac{n\pi x}{l}} od-ffwythiannau: f(-x)=-f(x) 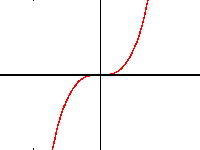Fig.: x^3, od-ffwythiant .
cyfres cosin Fourier 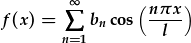f(x)=\sum_{n=1}^{\infty}b_n\cos{\frac{n\pi x}{l}} eil-ffwythiannau: f(-x)=f(x) 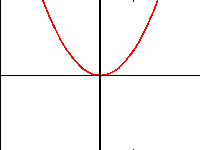Fig.: x^2, eil-ffwythiant.
cyfres Fourier cymhlyg 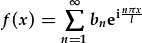f(x)=\sum_{n=1}^{\infty}b_ne^{i\frac{n\pi x}{l}} ffwythiannau eraill gyda chymuserudd eraill neu dim cymuserudd.

Esiampl: y gyfres sin

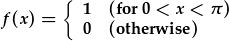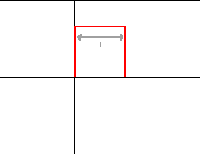Gan dybio fod gennym ffwythiant anghyfnodol, f(x)={1 (i 0\lt x\lt\pi); 0 (fel arall)}: Fig.: f(x), ffwythiant het Jac y Jwc..
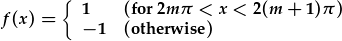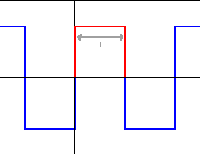Gallwn feddwl am y proffil hwn fel rhan o od-ffwythiant cyfnodol, g(x)={1 (i 2m\pi\lt x\lt (2m+1)\pi); -1 (arall)}: Fig.: g(x), ffwythiant cyfnodol yn osileiddio rhwng 1 a -1..

O fewn y cyfyngau lle ddiffinir f(x), f(x)=g(x), felly does dim ots beth sy'n cael ei adio tu allan i'r cyfyngiadau yma.

Gellir ffeindio cyfernodau y cyfres sin, 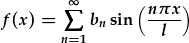f(x)=\sum_{n=1}^{\infty}b_n\sin{\frac{n\pi x}{l}},
trwy datrys yr integreiddiad 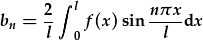b_n=\frac{2}{l}\int_0^lf(x)\sin{\frac{n\pi x}{l}}dx,
lle l yw hanner cyfnod yr osileiddiad ffwndamental (n=1).
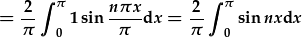Rhoi f(x) a l: =\frac{2}{\pi}\int_0^{\pi}1\sin{\frac{n\pi x}{\pi}dx}=\frac{2}{\pi}\int_0^{\pi}\sin{nx}dx,
integreiddio: =\frac{2}{n\pi}[\cos{nx}]_0^{\pi},
ac amnewid y cyfyngau: 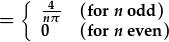={\frac{4}{n\pi} (n od); 0 (n gwastad)}.
Yn sgil hyn, gellir mynegi f(x) fel: 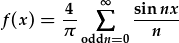f(x)=\frac{4}{\pi}\sum_{odd n=0}^{\infty}\frac{\sin{nx}}{n}
Fig.: Adeiladu ffwythiant het Jac y Jwc o termau Fourier.
Lawrllwytho y cyfres cyfan i un delwedd.

Mae'r ddelwedd ar y dde yn dangos y 5 term od cyntaf (n=1,3,5,7,9) a syt mae'n nhw'n graddol ffurfio siap ffwythiant het Jac y Jwc. Mae cyfernodau Fourier y termau gwastad yn sero fel y dangosir uchod. Mae'r termau Fourier unigol wedi eu plotio yn wyrdd, a'i swm yn las. Nodwch fod osgled pob term yn llai na'r term blaenorol, h.y. mae'r cywiriadau yn lleihau pob tro.

Gallwn nawr orffen datrys hafaliad Laplace.