Hafaliad ton 1 - datrysiad cyffredinol :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

Hafaliad ton yn ffiseg

Mae'r hafaliad don yn disgrifio prosesau ffisegol sy'n dilyn yr un patrwm yn gofod ac amser. Er enghraifft, os ydych yn plotio uchder arwynebedd y mor vs. safle llorweddol, mae'n don sin (neu cosin). Yn ogystal, os ydych yn plotio uchder y mor ar un pwynt mewn gofod vs. amser, mae hefyd yn don sin (neu cosin). Mae gofod ac amser yn gymuserol pan rydym yn ystyried osileiddiadau. Mae'r hafaliad don gyda ail ddeilliadau gyda pherthynas i gofod ac amser ill dau.

Rydym am ddatrys yr hafaliad don mewn un dimensiwn yn unig yma. Mae hyn yn cyfateb i symudiad llinyn sy'n dirgrynnu, y(x,t). Mewn dau ddimensiwn, e.e. mewn achos drwm, z(x,y,t), mae gofyn gwneud cam ychwanegol i wahanu newidion ar ol gwahanu'r rhan amser.

Datrysiad cyffredinol

Yn gyffredinol, gellir ysgrifennu'r hafaliad don fel:	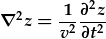$\nabla^2z=\frac{1}{v^2}\frac{\partial^2z}{\partial t^2}$ ,
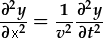neu, i gadw pethau'n syml, mewn 1D:	$\frac{\partial^2y}{\partial y^2}=\frac{1}{v^2}\frac{\partial^2y}{\partial t^2}$ .
Gan dybio datrysiad lluoswm:	y(x,t)=X(x)·T(t).
Amnewid lluoswm:	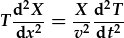$T\frac{d^2X}{dx^2}=\frac{X}{v^2}\frac{d^2T}{dt^2}$ ,
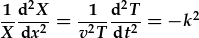gwahanu termau, a cyflwyno cysonyn gwahanu:	$\frac{1}{X}\frac{d^2X}{dx^2}=\frac{1}{v^2T}\frac{d^2T}{dt^2}=-k^2$ .
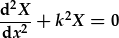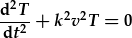Sy'n gadael dau HDC gyda cyfernodau cyson:	$\frac{d^2X}{dx^2}+k^2X=0$ ,	$\frac{d^2T}{dt^2}+k^2v^2T=0$
Y cyfernodau 2il radd yw:	a₂=1,	a₂=1,
y cyfernodau gradd 1af yw:	a₁=0,	a₁=0,
a'r cyfernodau gradd sero yw:	a₀=k²,	a₀=k²v².
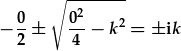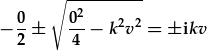Israddau'r polinomial rhinweddol yw:	$\frac{0}{2}\pm\sqrt{\frac{0^2}{4}-k^2}=\pm ik$ ,	$\frac{0}{2}\pm\sqrt{\frac{0^2}{4}-k^2v^2}=\pm ikv$ ,
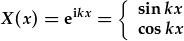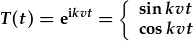a'r datrysiadau yw:	$X(x)=e^{ikx}={\sin{kx};\cos{kx}}$ ,	$T(t)=e^{ikvt}={\sin{kvt};\cos{kvt}}$ .

Nodwch fod y cysonyn k yr un fath yn y ddau ddatrysiad. Mae'r ddau yn esbonyddion cymhlyg, h.y. osiliadau, sy'n cytuno gyda arsylwadau o donnau ar llyn, fel y disgrifir uchod. Fel fod sin(kx) yn disgrifio'r osileiddiad gofodol, rhaid mesur k yn m^-1. Rhif ton yr osileiddiad yw. I gydbwyso'r unedau yn cos(kvt), rhaid i v fod yn m·s^-1; cyflymder y don yw. Yn ffiseg, mae'n arferol i ymuno'r ddau gysonyn a penodi'r amledd onglog, 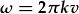$\omega=2\pi kv$ , yn lle.

Yn olaf, rhaid cyfuno'r ddau datrysiad rhannol. Felly'r datrysiadau cyffredinol i'r hafaliad don yw:

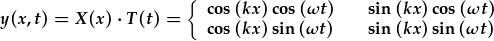
$y(x,t)=X(x)\cdot T(t)={\cos{(kx)}\cos{(\omega t)};\sin{(kx)}\cos{(\omega t)};\cos{(kx)}\sin{(\omega t)};\sin{(kx)}\sin{(\omega t)};}$

I gloi'r adran ar HDR, rhown esiampl arall sy'n defnyddio amodau terfyn i ffeindio datrysiadau o'r hafaliad don sy'n synhwyrol yn ffisegol ar gyfer problemau penodol.