Hafaliad Laplace 1 - Gwahanu newidion :: Mathemateg ar gyfer Ffisegwyr, ac i'r gwrthwyneb

Esiampl ffisegol

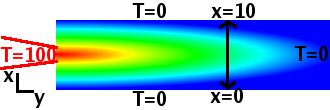
Fig.: Mae plat hir yn cael ei gynhesu ar un ochr, tra bod yr ochrau eraill yn oer.

Cynhesir plat tenau o hyd anfeidrol yng nghanol un ochr byr. Beth yw proffil y tymhereddT(x,y)?

Gan nad oes tardd o wres o fewn y plat, gellir defnyddio hafaliad Laplace:	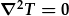$\nabla^2T=0$ ,
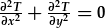sy'n fersiwn byr o:	$\frac{\partial^2T}{\partial x^2}+\frac{\partial^2T}{\partial y^2}=0$ .

Gwahanu'r newidion

Y cam cyntaf o ddatrys y HDR yw ei wahanu mewn i ddau HDC gyda pherthynas i'r ddau newidion annibynnol. I wneud hyn, rydym yn tybio fod modd ffeindio datrysiad drwy lluosi dau ffwythiant oun o'r ddau newidion yn unig: T(x,y)=X(x)Y(y). Mae priflythrennau yn dynodi ffwythiannau (newidion dibynnol), llythrennau bach yn cynrhychioli newidion annibynnol.

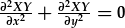Amnewid y dull lluoswm i'r HDR:	$\frac{\partial^2XY}{\partial x^2}+\frac{\partial^2XY}{\partial y^2}=0$ .
Nid yw Y(y) yn dibynnu ar x a gellir ei symud o flaen y differyn:	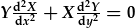$Y\frac{d^2X}{dx^2}+X\frac{d^2Y}{dy^2}=0$ ,
sy'n lleihau y differynnau i ddifferynnau cyffredin.
Rhannu gyda XY:	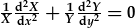$\frac{1}{X}\frac{d^2X}{dx^2}+\frac{1}{Y}\frac{d^2Y}{dy^2}=0$ .

Y ddadl yw yw fod y term ar y chwith yn dibynnu ar x yn unig, tra bod y term ar y dde yn dibynnu ar y yn unig. Er hyn, mae'n rhaid iddynt adio i sero i unrhyw cyfuniad o x and y. Mae hyn ond yn bosib os yw'r ddau yn gyson ac yn hafal (ond efo arwydd gwahanol). Mae'n gyfleus gosod -k² fel y cysonyn sy'n symleiddio y datrysiad yn y pen draw.

Gan ddilyn y dadl uchod,	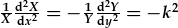$\frac{1}{X}\frac{d^2X}{dx^2}=-\frac{1}{Y}\frac{d^2Y}{dy^2}=-k^2$ .
Felly y x-HDC yw:	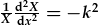$\frac{1}{X}\frac{d^2X}{dx^2}=-k^2$ ,
a'r y-HDC yw:	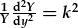$\frac{1}{Y}\frac{d^2Y}{dy^2}=k^2$ .

Mae'r ddau yn HDC llinol gyda cyfernodau cyson a gellir o ganlyniad eu datrys.

I barhau i ddatrys hafaliad Laplace, rydym angen gyntaf i ddarganfod syt i ddatrys HDC llinol o unrhyw radd gyda cyfernodau cyson.