Even and odd functions

When discussing the Fourier series, we have distinguished between even and odd functions because odd functions require only the sine terms and even functions require only the cosine terms in the series approximation. There is no need to calculate all the Fourier coefficients and find out that half of them are zero if we know that anyway. Therefore, exploiting symmetries can save some effort (or computing power).

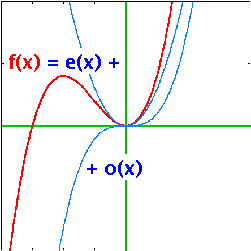Fig.: Even functions have mirror symmetry. Fig.: Odd functions have point symmetry. Fig.: All functions are a sum of an even and an odd part.
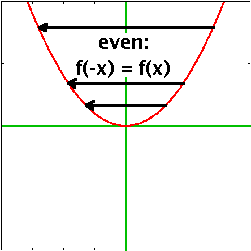
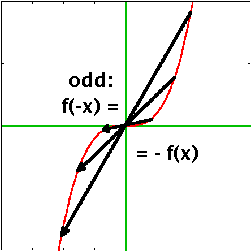
An even function is symmetric with respect to the y axis, i.e. if you fold the plot over along the y axis, the function maps onto itself. The value of the function at any negative value is the same as that at the corresponding positive value: f(-x) = f(x). Even powers are even functions (hence the name): x2, x4, x6... and so is cos(x). An odd function is one where the symmetry is one of inversion at the origin. Any point in the top right quadrant maps onto one at the bottom left etc., i.e. f(-x) = -f(x). Odd powers such as x, x3, x5... and sin(x) are odd functions. While, in general, functions are neither even nor odd, any function can be represented as a sum of an even and an odd part: f(x)=e(x)+o(x), where e(-x)=e(x) and o(-x)=-o(x).
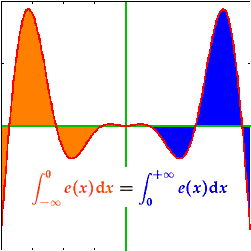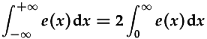Fig.: Integral of an even function. Because of its symmetry, the integral of the positive and the negative halves of an even function are the same (left), therefore \int_{-\infty}^{+\infty}e(x)dx=2\int_0^{\infty}e(x)dx.
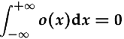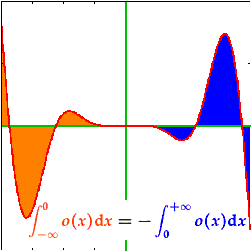On the other hand, the integrals of the positive and negative sides of an odd function (right) cancel out; i.e. \int_{-\infty}^{+\infty}o(x){\rm d}x = 0. 		Fig.: Integral of an odd function.
Multiplying even and odd functions is not like multiplying even and odd numbers:
even×even = even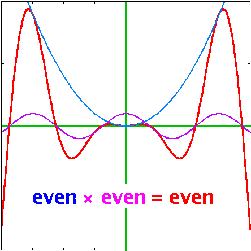
Fig.: Even times even is even. 		odd×odd = even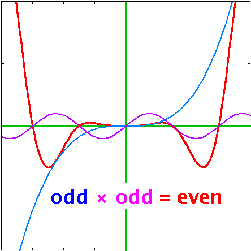
Fig.: Odd times odd is even. 		even×odd = odd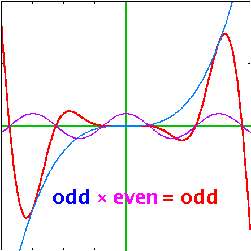
Fig.: Even times odd is odd.

Fourier transformation of even and odd functions

A general function is a sum of an even and an odd one: f(x) = e(x) + o(x)
The Fourier transform of f(x) is 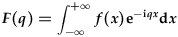F(q)=\int_{-\infty}^{+\infty}f(x)e^{-iqx}dx
or 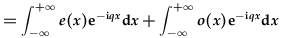=\int_{-\infty}^{+\infty}e(x)e^{-iqx}dx+\int_{-\infty}^{+\infty}o(x)e^{-iqx}dx.
Substitute the complex exponential: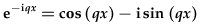
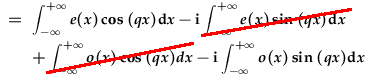(e^{-iqx}=\cos{qx}-i\sin{qx}) 		=\int_{-\infty}^{+\infty}e(x)\cos{qx}dx-i\int_{-\infty}^{+\infty}e(x)\sin{qx}dx+\int_{-\infty}^{+\infty}o(x)\cos{qx}dx-i\int_{-\infty}^{+\infty}o(x)\sin{qx}dx.
The functions e(x) and cos(x) are even, o(x) and sin(x) are odd. Therefore, the second and third integral integrate odd products, i.e. they evaluate as zero. The other two are integrals over even products.
So, by exploiting these symmetries: 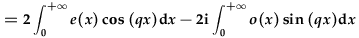=2\int_0^{+\infty}e(x)\cos{qx}dx-2i\int_0^{+\infty}o(x)\sin{qx}dx.

If the input function is even, i.e. o(x)=0, then the second term vanishes. Since e(x) depends only on x but not on q, the symmetry of the transform is determined by the term cos(qx), which is even in q.

Similarly, if f(x) is odd, i.e. e(x)=0, then the first term vanishes and the sin(qx) term makes the transform odd in q.

Even functions have even transforms; odd functions have odd transforms.

Note that, in general, both e(x) and o(x) are complex functions.

Real and imaginary functions

In general, both the input and the output functions of the Fourier transformation are complex functions. If either the imaginary or the real part of the input function is zero, this will result in a symmetric Fourier transform just as the even/odd symmetry does.

Do not confuse the terms imaginary and complex: A complex function has both real and imaginary parts, but the real part of an imaginary function is zero:
Real function: f(x) = re(x)
Imaginary function: f(x) = i im(x)
Complex function: f(x) = re(x) + i im(x)

If f(x) is a complex function, f(x) = re(x) + i im(x),
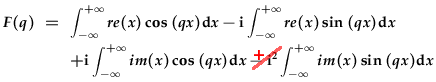the Fourier integral splits into four components: F(q)=\int_{-\infty}^{+\infty}re(x)\cos{qx}dx-i\int_{-\infty}^{+\infty}re(x)\sin{qx}dx+i\int_{-\infty}^{+\infty}im(x)\cos{qx}dx-i^2\int_{-\infty}^{+\infty}im(x)\sin{qx}dx,

so that integrals 1 and 4 constitute the real part of the transform, and integrals 2 and 3 its imaginary part.

Following the discussion of even/odd symmetry above, some of the integrals vanish if the input function has symmetries. For example, if the input function is real and odd, then im(x)=0 forces integrals 3 and 4 to zero. Of the remaining two integrals, number 1 is zero because the integrand is a product of an odd (re(x)) and an even (cos(x)) function. So, only integral 2 survives and F(q) is imaginary and odd.
The other combinations are:

If f(x) is... then only the ... integral survives and F(q) is...
real and even 1st real and even
real and odd 2nd imaginary and odd
imaginary and even 3rd imaginary and even
imaginary and odd 4th real and odd